【題目】在四棱錐
中，
底面
，底面為正方形，
，點
為正方形內部的一點，且
，則直線
與
所成角的余弦值的取值范圍為( )
A.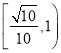
B.
C.
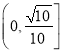D.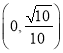
【答案】D
【解析】
根據題意，建立空間直角坐標系，在平面
上，由
計算
的軌跡方程，可知的軌跡是以
為圓心，以2為半徑的圓，在正方形中的部分；根據平行找直線
與
所成角的平面角，根據的軌跡判定臨界值，從而確定直線與所成角的余弦值的取值范圍.
由題意，以
為坐標原點，分別以
為
軸，建立空間直角坐標系，如圖所示，則有
，
設
，由，則列方程有
化簡得
，即點的軌跡是以為圓心，以2為半徑的圓，在正方形中的部分；
過作
垂足為
,連接
，則有
則直線與所成角的平面角為
，
則
根據點的軌跡是以為圓心，以2為半徑的圓，在正方形中的部分，
則點軌跡與正方形的邊交于一點
，記為
與正方形的
邊交于一點
，記為
當點從運動到位置時，
逐漸減小，逐漸增大，則的取值逐漸減小，
計算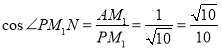
，
則直線與所成角的余弦值的取值范圍是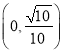
故選：
浙大優學小學年級銜接捷徑浙江大學出版社系列答案科目：高中數學 來源： 題型：
【題目】甲乙兩人報名參加由某網絡科技公司舉辦的“技能闖關”雙人電子競技比賽，比賽規則如下：每一輪“闖關”結果都采取計分制，若在一輪闖關中，一人過關另一人未過關，過關者得1分，未過關得
分；若兩人都過關或都未過關則兩人均得0分.甲、乙過關的概率分別為
和
，在一輪闖關中，甲的得分記為
.
（1）求的分布列；
（2）為了增加趣味性，系統給每位報名者基礎分3分，并且規定出現一方比另一方多過關三輪者獲勝，此二人比賽結束.
表示“甲的累積得分為
時，最終認為甲獲勝”的概率，則
，其中
，
，
，令
.證明：點
的中點橫坐標為
；
（3）在第（2）問的條件下求
，并嘗試解釋游戲規則的公平性.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列
是遞減的等差數列，的前
項和是
，且
，有以下四個結論：
①
；
②若對任意
都有
成立，則
的值等于7或8時；
③存在正整數，使
；
④存在正整數
，使
．
其中所有正確結論的序號是
A. ①②B. ①②③
C. ②③④D. ①②③④
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系xOy中，以坐標原點為極點，x軸的正半軸為極軸建立極坐標系，曲線
的極坐標方程為
，P是曲線上的動點，M為線段OP的中點，設點M的軌跡為曲線
．
（1）求的極坐標方程；
（2）若射線
與曲線異于極點的交點為A，與曲線異于極點的交點為B，求
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，四棱錐
的底面是菱形，
底面
，
分別是
的中點，
，
，
.
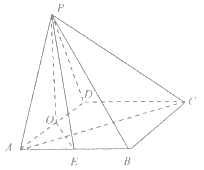
（I）證明：
；
（II）求直線
與平面
所成角的正弦值；
（III）在
邊上是否存在點
，使
與
所成角的余弦值為
，若存在，確定點位置；若不存在，說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
