
分析 (1)通過構造函數,利用函數的導數,通過函數的單調性以及函數的最值推出結果,
(2)由(1)的結論可得ln$\frac{k+1}{k}$>$\frac{2}{2k+1}$,根據對數的運算性質和迭代法即可得到ln(n+1)=ln$\frac{2}{1}$+ln$\frac{3}{2}$+…+ln$\frac{n+1}{n}$>$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{2}{2n+1}$,問題得以證明
解答 解:(1)f(x)=lnx+$\frac{2}{x+1}$的定義域為(0,+∞),
令h(x)=f(x)-1=lnx+$\frac{2}{x+1}$-1,
則h′(x)=$\frac{1}{x}$-$\frac{2}{(x+1)^{2}}$=$\frac{{x}^{2}+1}{x(x+1)^{2}}$>0,
∴h(x)在(0,+∞)為增函數,
當x>1時,h(x)>h(1)=0,即f(x)>1當0<x<1時,h(x)<h(1)=0,即f(x)>1,
當x=1時,h(x)=h(1)=0,即f(1)=0,
(2)根據(1)的結論,當x>1時,
lnx+$\frac{2}{x+1}$>1,即lnx>$\frac{x-1}{x+1}$,
令x=$\frac{k+1}{k-1}$,k∈N*,
即ln$\frac{k+1}{k}$>$\frac{\frac{k+1}{k}-1}{\frac{k+1}{k}+1}$=$\frac{2}{2k+1}$,
∴ln(n+1)=ln$\frac{2}{1}$+ln$\frac{3}{2}$+…+ln$\frac{n+1}{n}$>$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{2}{2n+1}$,
即ln(n+1)>$\frac{1}{3}$+$\frac{1}{5}$+$\frac{1}{7}$+…+$\frac{1}{2n+1}(n∈{N^*})$.
點評 本題考查了利用導數研究函數的單調性極值最值,考查了利用已經證明的結論證明不等式的方法,考查了推理能力與計算能力,屬于難題.


 考前必練系列答案
考前必練系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
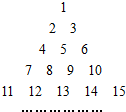 將全體正整數排成一個三角形數陣:按照如圖所示排列的規律:
將全體正整數排成一個三角形數陣:按照如圖所示排列的規律:查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -5 | B. | -7 | C. | -9 | D. | -11 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com