
分析 由題意可設橢圓的標準方程為:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0).根據過F1作弦AB,且△ABF2的周長為20,則4a=20,解得a,又c=4,則$b=\sqrt{{a}^{2}-{c}^{2}}$,即可得出.
解答 解:由題意可設橢圓的標準方程為:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0).
∵過F1作弦AB,且△ABF2的周長為20,則4a=20,解得a=5,
又c=4,則$b=\sqrt{{a}^{2}-{c}^{2}}$=3.
∴橢圓的標準方程為:$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{9}$=1.
故答案為:$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{9}$=1.
點評 本題考查了橢圓的定義標準方程及其性質,考查了推理能力與計算能力,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
 如圖給出一個“三角形數陣”,已知每一列的數成等差數列,從第三行起,每一行的數成等比數列,每一行的公比都相等,記第i行第j列的數為${a_{ij}}(i≥j,i,j∈{N^*})$,則a63=( )
如圖給出一個“三角形數陣”,已知每一列的數成等差數列,從第三行起,每一行的數成等比數列,每一行的公比都相等,記第i行第j列的數為${a_{ij}}(i≥j,i,j∈{N^*})$,則a63=( )| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 654 | B. | 656 | C. | 658 | D. | 660 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
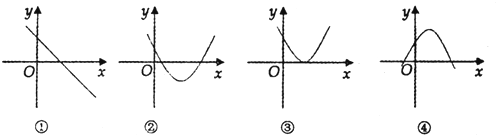
| A. | ①③ | B. | ②③ | C. | ①②④ | D. | ②④ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com