
平面內(nèi)有向量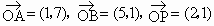 ,點Q為直線OP上的一個動點.
,點Q為直線OP上的一個動點.
(1)當(dāng) 取最小值時,求
取最小值時,求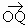 的坐標(biāo);
的坐標(biāo);
(2)當(dāng)點Q滿足(1)的條件和結(jié)論時,求cos∠AQB的值.
|
解: (1)設(shè)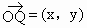 , ,
∵ Q在直線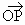 上,∴向量 上,∴向量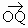 與 與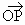 共線. 共線.
又 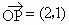 , ,
∴ x-2y=0,∴x=2y,∴ 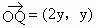 , ,
又 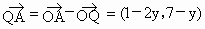 , ,
∴
故當(dāng)y=2時, 此時 (2)由(1)知:
因為點 Q在直線OP上,向量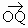 與 與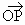 共線,可以得到關(guān)于OQ坐標(biāo)的一個關(guān)系式,再根據(jù) 共線,可以得到關(guān)于OQ坐標(biāo)的一個關(guān)系式,再根據(jù)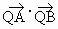 最小,求得 最小,求得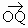 ,進(jìn)而求出cos∠AQB. ,進(jìn)而求出cos∠AQB. |
|
已知兩向量的坐標(biāo),由平面向量數(shù)量積的定義和性質(zhì)可求其數(shù)量積、兩向量的模和它們的夾角,此外,求解數(shù)量積的有關(guān)綜合問題,注意利用函數(shù)思想、方程思想求解. |


 A加金題 系列答案
A加金題 系列答案 全優(yōu)測試卷系列答案
全優(yōu)測試卷系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源:張家界市一中2007屆高三4月模擬考試?yán)砜茢?shù)學(xué)試卷 題型:044
平面內(nèi)有向量![]() =(1,7),
=(1,7),![]() =(5,1),
=(5,1),![]() =(2,1),點Q為直線OP上的一個動點.
=(2,1),點Q為直線OP上的一個動點.

(1)當(dāng)![]() ·
·![]() 取最小值時,求
取最小值時,求![]() 的坐標(biāo);
的坐標(biāo);
(2)當(dāng)點Q滿足(1)的條件和結(jié)論時,求cos∠AQB的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:044
平面內(nèi)有向量 ,點Q為直線OP上的一個動點.
,點Q為直線OP上的一個動點.
(1)當(dāng) 取最小值時,求
取最小值時,求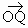 的坐標(biāo);
的坐標(biāo);
(2)當(dāng)點Q滿足(1)的條件和結(jié)論時,求cos∠AQB的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(1)當(dāng)![]() ·
·![]() 取最小值時,求
取最小值時,求![]() 的坐標(biāo);
的坐標(biāo);
(2)當(dāng)點Q滿足(1)的條件和結(jié)論時,求cos∠AQB的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(1)當(dāng)![]() ·
·![]() 取最小值時,求
取最小值時,求![]() 的坐標(biāo);
的坐標(biāo);
(2)當(dāng)點Q滿足(1)的條件和結(jié)論時,求cos∠AQB的值.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com