
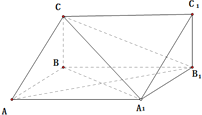
【題目】如圖,三棱柱![]() 中,四邊形
中,四邊形![]() 是菱形,
是菱形,![]() ,二面角
,二面角![]() 為
為![]() ,
, ![]() .
.
(Ⅰ)求證:平面![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)見解析(2)![]()
【解析】試題分析:(1)先由三棱柱性質將線面垂直![]() 轉化為
轉化為![]() ,再由
,再由![]() 得線線垂直
得線線垂直![]() ,又由
,又由![]() 是菱形得
是菱形得![]() ,最后根據線面垂直判定定理得線面垂直
,最后根據線面垂直判定定理得線面垂直![]() , 根據面面垂直判定定理得平面
, 根據面面垂直判定定理得平面![]() 平面
平面![]() .(2)求二面角的大小,一般借助空間向量數量積求解,先根據條件建立空間直角坐標系,設立各點坐標,利用方程組解出各面法向量,利用向量數量積求兩法向量夾角,最后根據二面角與法向量夾角關系求二面角.
.(2)求二面角的大小,一般借助空間向量數量積求解,先根據條件建立空間直角坐標系,設立各點坐標,利用方程組解出各面法向量,利用向量數量積求兩法向量夾角,最后根據二面角與法向量夾角關系求二面角.
試題解析:(1)證明:在三棱柱![]() 中,由
中,由![]()
得![]() ,則
,則![]() ,
,
又![]() 是菱形, 得
是菱形, 得![]() ,而
,而![]() ,
,
則![]() ,
,
故平面![]() 平面
平面![]() .
.
(2)
由題意得![]() 為正三角形,
為正三角形,
取![]() 得中點為D,連CD,BD,
得中點為D,連CD,BD,
則![]() ,又
,又![]()
易得![]() ,則
,則![]() 為二面角
為二面角![]() 的平面角,
的平面角,
因![]() ,
, ![]() =
=![]() ,所以
,所以![]() ,
,
所以![]()
過![]() 交點
交點![]() 作
作![]() ,垂足為
,垂足為![]() ,連
,連![]()
則![]() 為二面角
為二面角![]() 的平面角,
的平面角,
又![]() 得
得![]()
所以![]()
另:建系用向量法相應給分。


科目:高中數學 來源: 題型:
【題目】已知由甲、乙兩位男生和丙、丁兩位女生組成的四人沖關小組,參加由安徽衛視推出的大型戶外競技類活動《男生女生向前沖》.活動共有四關,若四關都闖過,則闖關成功,否則落水失敗.設男生闖過一至四關的概率依次是![]() ,女生闖過一至四關的概率依次是
,女生闖過一至四關的概率依次是![]() .
.
(Ⅰ)求男生甲闖關失敗的概率;
(Ⅱ)設![]() 表示四人沖關小組闖關成功的人數,求隨機變量
表示四人沖關小組闖關成功的人數,求隨機變量![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=|ex﹣a|+| ![]() ﹣1|,其中a,x∈R,e是自然對數的底數,e=2.71828…
﹣1|,其中a,x∈R,e是自然對數的底數,e=2.71828…
(1)當a=0時,解不等式f(x)<2;
(2)求函數f(x)的單調增區間;
(3)設a≥ ![]() ,討論關于x的方程f(f(x))=
,討論關于x的方程f(f(x))= ![]() 的解的個數.
的解的個數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() :
: ![]() 與
與![]() 軸的交點是橢圓
軸的交點是橢圓![]() :
: ![]() 的一個焦點.
的一個焦點.
(1)求橢圓![]() 的方程;
的方程;
(2)若直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 、
、![]() 兩點,是否存在
兩點,是否存在![]() 使得以線段
使得以線段![]() 為直徑的圓恰好經過坐標原點
為直徑的圓恰好經過坐標原點![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】1979年,李政道博士給中國科技大學少年班出過一道智趣題:5只猴子分一堆桃子,怎么也不能分成5等份,只好先去睡覺,準備第二天再分,夜里1只猴子偷偷爬起來,先吃掉一個桃子,然后將其分成5等份,藏起自己的一份就去睡覺了;第2只猴子又爬起來,將剩余的桃子吃掉一個后,也將桃子分成5等份;藏起自己的一份睡覺去了;以后的3只猴子都先后照此辦理,問:最初至少有多少個桃子?最后至少剩下多少個桃子?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某運動員每次投籃命中的概率等于40%.現采用隨機模擬的方法估計該運動員三次投籃恰有兩次命中的概率:先由計算器產生0到9之間取整數值的隨機數,指定1,2,3,4表示命中,5,6,7,8,9,0,表示不命中;再以每三個隨機數為一組,代表三次投籃的結果.經隨機模擬產生了如下2-組隨機數:
907 966 191 925 271 932 812 458
569 683 431 257 393 027 556 488
730 113 537 989
據此估計,該運動員三次投籃恰有兩次命中的概率為__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近幾年來,我國許多地區經常出現干旱現象,為抗旱經常要進行人工降雨,現由天氣預報得知,某地在未來5天的指定時間的降雨概率是:前3天均為![]() ,后2天均為
,后2天均為![]() ,5天內任何一天的該指定時間沒有降雨,則在當天實行人工降雨,否則,當天不實施人工降雨.
,5天內任何一天的該指定時間沒有降雨,則在當天實行人工降雨,否則,當天不實施人工降雨.
(1)求至少有1天需要人工降雨的概率;
(2)求不需要人工降雨的天數![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com