
【題目】近幾年來,我國許多地區經常出現干旱現象,為抗旱經常要進行人工降雨,現由天氣預報得知,某地在未來5天的指定時間的降雨概率是:前3天均為![]() ,后2天均為
,后2天均為![]() ,5天內任何一天的該指定時間沒有降雨,則在當天實行人工降雨,否則,當天不實施人工降雨.
,5天內任何一天的該指定時間沒有降雨,則在當天實行人工降雨,否則,當天不實施人工降雨.
(1)求至少有1天需要人工降雨的概率;
(2)求不需要人工降雨的天數![]() 的分布列和期望.
的分布列和期望.
【答案】(1)![]() (2) x的分布列是:
(2) x的分布列是:
x | 0 | 1 | 2 | 3 | 4 | 5 |
P |
|
|
|
|
|
|
3.1
【解析】(1)5天全不需要人工降雨的概率是P1=()3·()2=![]() ,故至少有1天需要人工降雨的概率是1-P1=1-
,故至少有1天需要人工降雨的概率是1-P1=1-![]() =
=![]() .
.
(2)x的取值是0,1,2,3,4,5,由(1)知5天不需要人工降雨的概率是:P(x=5)=P1=![]() ,
,
4天不需要人工降雨的概率是:
P(x=4)=()3![]() ×+
×+![]() ()3()2=
()3()2=![]()
=![]() ,
,
3天不需要人工降雨的概率是:
P(x=3)=![]() ()3()2+
()3()2+![]() ()3
()3![]() ()()+()3()2=
()()+()3()2=![]() ,
,
2天不需要人工降雨的概率是:
P(x=2)=![]() ()3()2+
()3()2+![]() ()3
()3![]() ()×()+()3×()2=
()×()+()3×()2=![]() ,
,
1天不需要人工降雨的概率是:
P(x=1)=![]() ()3()2+()3
()3()2+()3![]() ()()=
()()=![]() ,
,
0天不需要人工降雨的概率是:
P(x=0)=()3()2=![]() ,
,
故不需要人工降雨的天數x的分布列是:
x | 0 | 1 | 2 | 3 | 4 | 5 |
P |
|
|
|
|
|
|
不需要人工降雨的天數x的期望是:
E(x)=0×![]() +1×
+1×![]() +2×
+2×![]() +3×
+3×![]() +4×
+4×![]() +5×
+5×![]() =3.1.
=3.1.
【方法技巧】求離散型隨機變量均值與方差的基本方法
(1)定義法:已知隨機變量的分布列求它的均值、方差和標準差,可直接按定義(公式)求解.
(2)性質法:已知隨機變量ξ的均值與方差,求ξ的線性函數η=aξ+b的均值與方差,可直接利用均值、方差的性質求解.
(3)公式法:如能分析所給隨機變量是服從常用的分布(如兩點分布,二項分布等),可直接利用它們的均值、方差公式求解.


科目:高中數學 來源: 題型:
【題目】某產品的廣告費用x與銷售額y的統計數據如表:
廣告費用x(萬元) | 4 | 2 | 3 | 5 |
銷售額y(萬元) | 49 | 26 | 39 | 54 |
根據上表可得回歸方程 ![]() =
= ![]() x+
x+ ![]() 中的
中的 ![]() 為9.4,據此模型預報廣告費用為6萬元時銷售額為( )
為9.4,據此模型預報廣告費用為6萬元時銷售額為( )
A.63.6萬元
B.67.7萬元
C.65.5萬元
D.72.0萬元
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 的焦點在
的焦點在![]() 軸上,橢圓
軸上,橢圓![]() 的左頂點為
的左頂點為![]() ,斜率為
,斜率為![]() 的直線交橢圓
的直線交橢圓![]() 于
于![]() ,
, ![]() 兩點,點
兩點,點![]() 在橢圓
在橢圓![]() 上,
上, ![]() ,直線
,直線![]() 交
交![]() 軸于點
軸于點![]() .
.
(Ⅰ)當點![]() 為橢圓的上頂點,
為橢圓的上頂點, ![]() 的面積為
的面積為![]() 時,求橢圓的離心率;
時,求橢圓的離心率;
(Ⅱ)當![]() ,
, ![]() 時,求
時,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的中心在原點,離心率等于
的中心在原點,離心率等于![]() ,它的一個短軸端點恰好是拋物線
,它的一個短軸端點恰好是拋物線![]() 的焦點
的焦點
(1)求橢圓![]() 的方程;
的方程;
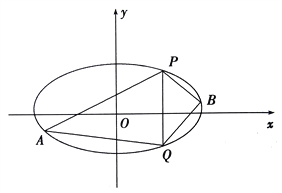
(2)已知![]() 、
、![]() 是橢圓上的兩點,
是橢圓上的兩點, ![]() ,
, ![]() 是橢圓上位于直線
是橢圓上位于直線![]() 兩側的動點.①若直線
兩側的動點.①若直線![]() 的斜率為
的斜率為![]() ,求四邊形
,求四邊形![]() 面積的最大值;
面積的最大值;
②當![]() ,
, ![]() 運動時,滿足
運動時,滿足![]() ,試問直線
,試問直線![]() 的斜率是否為定值,請說明理由
的斜率是否為定值,請說明理由
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等差數列{an}的公差d>0,設{an}的前n項和為Sn , a1=1,S2S3=36.
(1)求d及Sn;
(2)求m,k(m,k∈N*)的值,使得am+am+1+am+2+…+am+k=65.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 且
且![]() ,直線:
,直線: ![]() ,圓
,圓![]() :
:![]()
![]() .
.
(Ⅰ)若![]() ,請判斷直線與圓
,請判斷直線與圓![]() 的位置關系;
的位置關系;
(Ⅱ)求直線傾斜角![]() 的取值范圍;
的取值范圍;
(Ⅲ)直線能否將圓![]() 分割成弧長的比值為
分割成弧長的比值為![]() 的兩段圓弧?為什么?
的兩段圓弧?為什么?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分為14分)已知定義域為R的函數![]() 是奇函數.
是奇函數.
(1)求a,b的值;
(2)若對任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com