【題目】已知某款冰淇淋的包裝盒為圓臺，盒蓋為直徑為
的圓形紙片，每盒冰淇淋中包含有香草口味、巧克力口味和草莓口味冰淇淋球各一個，假定每個冰淇淋球都是半徑為
的球體，三個冰淇淋球兩兩相切，且都與冰淇淋盒蓋、盒底和盒子側面的曲面相切，則冰淇淋盒的體積為______．
科目：高中數學 來源： 題型：
【題目】在平行四邊形
中，
，
，過
點作
的垂線，交的延長線于點
，
.連結
，交
于點
，如圖1，將
沿折起，使得點到達點
的位置，如圖2.
（1）證明：平面
平面
；
（2）若
為
的中點，
為的中點，且平面
平面，求三棱錐
的體積.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知某地區某種昆蟲產卵數和溫度有關.現收集了一只該品種昆蟲的產卵數
（個）和溫度
（
）的7組觀測數據，其散點圖如所示：
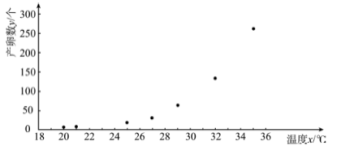
根據散點圖，結合函數知識，可以發現產卵數和溫度可用方程
來擬合，令
，結合樣本數據可知
與溫度可用線性回歸方程來擬合．根據收集到的數據，計算得到如下值：
|
|
|
|
|
|
27 | 74 |
| 182 |
|
|
表中
，
．
（1）求和溫度的回歸方程（回歸系數結果精確到
）；
（2）求產卵數關于溫度的回歸方程；若該地區一段時間內的氣溫在
之間（包括
與
），估計該品種一只昆蟲的產卵數的范圍.（參考數據：
，
，
，
，
．）
附：對于一組數據
，
，…，
，其回歸直線
的斜率和截距的最小二乘估計分別為
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】2019年10月，德國爆發出“芳香烴門”事件，即一家權威的檢測機構在德國銷售的奶粉中隨機抽檢了16款(德國4款，法國8款，荷蘭4款)，其中8款檢測出芳香烴礦物油成分，此成分會嚴重危害嬰幼兒的成長，有些奶粉已經遠銷至中國．A地區聞訊后，立即組織相關檢測員對這8款品牌的奶粉進行抽檢，已知該地區有6家嬰幼兒用品商店在售這幾種品牌的奶粉，甲、乙、丙3名檢測員分別負責進行檢測，每人至少抽檢1家商店，且檢測過的商店不重復檢測，則甲檢測員檢測2家商店的概率為（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】法國數學家布豐提出一種計算圓周率
的方法——隨機投針法，受其啟發，我們設計如下實驗來估計的值：先請200名同學每人隨機寫下一個橫、縱坐標都小于1的正實數對
；再統計兩數的平方和小于1的數對的個數
；最后再根據統計數來估計的值.已知某同學一次試驗統計出
，則其試驗估計為______.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，橢圓
的離心率是
，左右焦點分別為
，
，過點
的動直線
與橢圓相交于
，
兩點，當直線過時，
的周長為
.
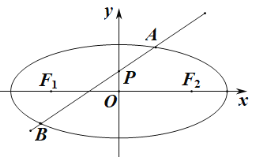
（1）求橢圓
的方程；
（2）當
時，求直線方程；
（3）已知點
，直線
，
的斜率分別為
，
.問是否存在實數
，使得
恒成立？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的左右焦點為
，過
（M不過橢圓的頂點和中心）且斜率為k直線l交橢圓于
兩點，與y軸交于點N，且
.
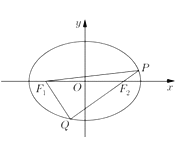
（1）若直線l過點
，求
的周長；
（2）若直線l過點，求線段
的中點R的軌跡方程；
（3）求證：
為定值，并求出此定值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】直線l：ax+
y﹣1=0與x，y軸的交點分別為A，B，直線l與圓O：x2+y2=1的交點為C，D，給出下面三個結論：①a≥1，S△AOB=
；②a≥1，|AB|＜|CD|；③a≥1，S△COD＜.其中，所有正確結論的序號是（ ）
A.①②B.②③C.①③D.①②③
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列
，記集合
.
（1）對于數列
，寫出集合
；
（2）若
，是否存在
，使得
？若存在，求出一組符合條件的
；若不存在，說明理由.
（3）若
，把集合中的元素從小到大排列，得到的新數列為
，若
，求
的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
