
(本小題滿分14分)已知橢圓C: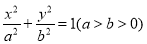 的焦距為4,其長軸長和短軸長之比為
的焦距為4,其長軸長和短軸長之比為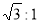 .
.
(Ⅰ)求橢圓C的標準方程;
(Ⅱ)設F為橢圓C的右焦點,T為直線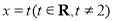 上縱坐標不為0的任意一點,過F作TF的垂線交橢圓C于點P,Q.
上縱坐標不為0的任意一點,過F作TF的垂線交橢圓C于點P,Q.
(ⅰ)若OT平分線段PQ(其中O為坐標原點),求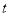 的值;
的值;
(ⅱ)在(ⅰ)的條件下,當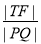 最小時,求點T的坐標.
最小時,求點T的坐標.
(Ⅰ)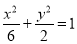 ;(Ⅱ)(ⅰ)
;(Ⅱ)(ⅰ)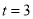 ;(ⅱ)當
;(ⅱ)當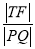 最小時,T點的坐標是(3,1)或(3,-1).
最小時,T點的坐標是(3,1)或(3,-1).
【解析】
試題分析:(Ⅰ)利用條件“焦距為4,其長軸長和短軸長之比為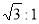 ”列方程求出
”列方程求出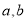 的值從而確定橢圓的標準方程.
的值從而確定橢圓的標準方程.
(Ⅱ)(ⅰ)由(Ⅰ)可得,F點的坐標是(2,0). 設直線PQ的方程為x=my+2,將直線PQ的方程與橢圓C的方程聯立,得 消去
消去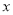 得到關于
得到關于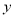 的一元二次方程,于是可利用韋達定理與兩直線的位置關系確定
的一元二次方程,于是可利用韋達定理與兩直線的位置關系確定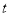 的值.(ⅱ)由(ⅰ)知T為直線
的值.(ⅱ)由(ⅰ)知T為直線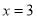 上任意一點可得,點T點的坐標為
上任意一點可得,點T點的坐標為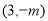 .利用兩點間的距離公式將
.利用兩點間的距離公式將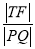 表示成
表示成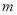 的函數,最后利用函數或不等式的方法求出其取得最小值時的
的函數,最后利用函數或不等式的方法求出其取得最小值時的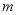 值,從而確定T點的縱坐標..
值,從而確定T點的縱坐標..
試題解析:【解析】
(Ⅰ)由已知可得 解得a2=6,b2=2.
解得a2=6,b2=2.
所以橢圓C的標準方程是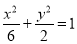 . (4分)
. (4分)
(Ⅱ)(ⅰ)由(Ⅰ)可得,F點的坐標是(2,0).
設直線PQ的方程為x=my+2,將直線PQ的方程與橢圓C的方程聯立,得
消去x,得(m2+3)y2+4my-2=0,其判別式Δ=16m2+8(m2+3)>0.
設P(x1,y1),Q(x2,y2),則y1+y2=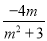 ,y1y2=
,y1y2=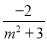 .于是x1+x2=m(y1+y2)+4=
.于是x1+x2=m(y1+y2)+4=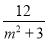 .
.
設M為PQ的中點,則M點的坐標為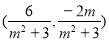 .
.
因為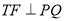 ,所以直線FT的斜率為
,所以直線FT的斜率為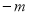 ,其方程為
,其方程為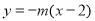 .
.
當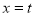 時,
時,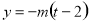 ,所以點
,所以點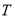 的坐標為
的坐標為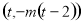 ,
,
此時直線OT的斜率為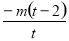 ,其方程為
,其方程為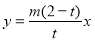 .
.
將M點的坐標為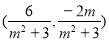 代入,得
代入,得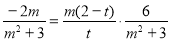 .
.
解得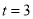 . (8分)
. (8分)
(ⅱ)由(ⅰ)知T為直線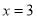 上任意一點可得,點T點的坐標為
上任意一點可得,點T點的坐標為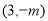 .
.
于是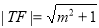 ,
,
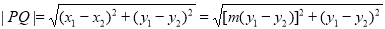
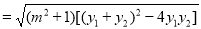
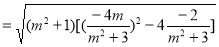

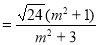 .
.
所以
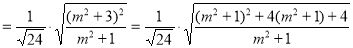
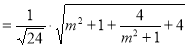
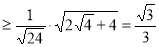 .
.
當且僅當m2+1=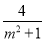 ,即m=±1時,等號成立,此時
,即m=±1時,等號成立,此時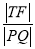 取得最小值
取得最小值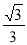 .
.
故當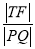 最小時,T點的坐標是(3,1)或(3,-1). (14分)
最小時,T點的坐標是(3,1)或(3,-1). (14分)
考點:1、橢圓的標準方程;2、直線與橢圓的位置關系綜合問題.


科目:高中數學 來源:2014-2015學年河北省高一12月月考數學試卷(解析版) 題型:選擇題
已知點P在正方形ABCD所在平面外,PA⊥平面ABCD,PA=AB,則PB與AC所成的角是( )
A.90° B.60° C.45° D.30°
查看答案和解析>>
科目:高中數學 來源:2014-2015學年湖南省株洲市高三教學質量統一檢測一理科數學試卷(解析版) 題型:選擇題
已知底面為正方形的四棱錐,其一條側棱垂直于底面,那么該四棱錐的三視圖可能是下列各圖中的( )

查看答案和解析>>
科目:高中數學 來源:2014-2015學年湖北省武漢市武昌區高三元月調研考試文科數學試卷(解析版) 題型:填空題
已知某地區中小學生人數和近視情況如下表所示:
年級 | 人數 | 近視率 |
小學 | 3500 | 10% |
初中 | 4500 | 30% |
高中 | 2000 | 50% |
為了解該地區中小學生的近視形成原因,用分層抽樣的方法抽取2%的學生進行調查,
則:(Ⅰ)樣本容量為___________;(Ⅱ)抽取的高中生中,近視人數為___________.
查看答案和解析>>
科目:高中數學 來源:2014-2015學年湖北省武漢市武昌區高三元月調研考試文科數學試卷(解析版) 題型:選擇題
根據如下樣本數據
x | 3 | 4 | 5 | 6 | 7 |
y | 4.0 | 2.5 |
| 0.5 |
|
得到的回歸方程為 .若
.若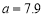 ,則
,則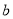 的值為
的值為
A. B.
B.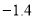 C.
C.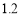 D.
D.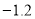
查看答案和解析>>
科目:高中數學 來源:2014-2015學年湖北省武漢市武昌區高三元月調研考試理科數學試卷(解析版) 題型:填空題
已知曲線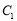 的參數方程是
的參數方程是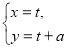 (
(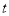 為參數,a為實數常數),曲線
為參數,a為實數常數),曲線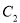 的參數方程是
的參數方程是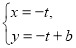 (
(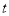 為參數,b為實數常數).以坐標原點為極點,
為參數,b為實數常數).以坐標原點為極點,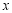 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線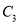 的極坐標方程是
的極坐標方程是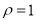 . 若
. 若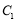 與
與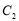 分曲線
分曲線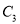 所成長度相等的四段弧,則
所成長度相等的四段弧,則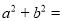 .
.
查看答案和解析>>
科目:高中數學 來源:2014-2015學年湖北省武漢市武昌區高三元月調研考試理科數學試卷(解析版) 題型:選擇題
拋物線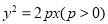 的焦點為
的焦點為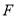 ,準線為
,準線為 ,
,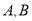 是拋物線上的兩個動點,且滿足
是拋物線上的兩個動點,且滿足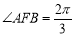 .設線段
.設線段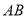 的中點
的中點 在
在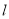 上的投影為
上的投影為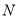 ,則
,則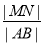 的最大值是
的最大值是
A.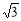 B.
B.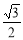 C.
C.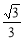 D.
D.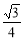
查看答案和解析>>
科目:高中數學 來源:2014-2015學年浙江省高一上學期第二次月考數學試卷(解析版) 題型:填空題
設函數f(x)=ax,(a>0且a≠1),對于任意x,y∈R,下列算式中:
①f(x+y)=f(x)·f(y);
②f(xy)=f(x)+f(y);
③f(x-y)= ;
;
④ ;
;
⑤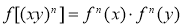 , 其中不正確的是__ .(填上所有不正確的題號)
, 其中不正確的是__ .(填上所有不正確的題號)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com