
(1)寫出函數y=x2-2x的單調區間及其圖像的對稱軸,觀察:在函數圖像對稱軸兩側的單調性有什么特點?
(2)寫出函數y=|x|的單調區間及其圖像的對稱軸,觀察:在函數圖像對稱軸兩側的單調性有什么特點?
(3)定義在[-4,8]上的函數y=f(x)的圖像關于直線x=2對稱,y=f(x)的部分圖像如圖所示,請補全函數y=f(x)的圖像,并寫出其單調區間,觀察:在函數圖像對稱軸兩側的單調性有什么特點?

(4)由以上你發現了什么結論?試加以證明.
解:(1)函數y=x2-2x的單調遞減區間是(-∞,1),單調遞增區間是(1,+∞);對稱軸是直線x=1;區間(-∞,1)和區間(1,+∞)關于直線x=1對稱,單調性相反.
(2)函數y=|x|的單調遞減區間是(-∞,0),單調遞增區間是(0,+∞);對稱軸是y軸即直線x=0;區間(-∞,0)和區間(0,+∞)關于直線x=0對稱,單調性相反.
(3)函數y=f(x),x∈[-4,8]的圖像如圖所示.
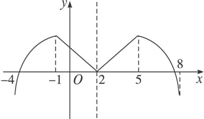
函數y=f(x)的單調遞增區間是[-4,-1],[2,5];單調遞減區間是[5,8],[-1,2];區間[-4,-1]和區間[5,8]關于直線x=2對稱,單調性相反,區間[-1,2]和區間[2,5]關于直線x=2對稱,單調性相反.
(4)可以發現結論:如果函數y=f(x)的圖像關于直線x=m對稱,那么函數y=f(x)在直線x=m兩側對稱單調區間內具有相反的單調性.證明如下:
不妨設函數y=f(x)在對稱軸直線x=m的右側一個區間[a,b]上是增函數,區間[a,b]關于直線x=m的對稱區間是[2m-b,2m-a].
由于函數y=f(x)的圖像關于直線x=m對稱,則f(x)=f(2m-x).
設2m-b≤x1<x2≤2m-a,則b≥2m-x1>2m-x2≥a,
f(x1)-f(x2)=f(2m-x1)-f(2m-x2).
又∵函數y=f(x)在[a,b]上是增函數,∴f(2m-x1)-f(2m-x2)>0.
∴f(x1)-f(x2)>0.
∴f(x1)>f(x2).
∴函數y=f(x)在區間[2m-b,2m-a]上是減函數.
∴當函數y=f(x)在對稱軸直線x=m的右側一個區間[a,b]上是增函數時,在[a,b]關于直線x=m的對稱區間[2m-b,2m-a]上則是減函數,即單調性相反.
因此有結論:如果函數y=f(x)的圖像關于直線x=m對稱,那么函數y=f(x)在對稱軸兩側的對稱單調區間內具有相反的單調性.
本題探討函數的單調性的性質.利用歸納、猜想、證明的方法得到結論,用定義證明結論.


 口算能手系列答案
口算能手系列答案科目:高中數學 來源:高考零距離 二輪沖刺優化講練 數學 題型:044
| |||||||||||
查看答案和解析>>
科目:高中數學 來源:順德北滘中學2007年高考數學(文科)綜合模擬試卷(二) 題型:044
f(x)是定義在[-2π,2π]上的偶函數,當x![]() [0,π]時,f(x)=cosx,當x
[0,π]時,f(x)=cosx,當x![]() (π,2π]時,y=f(x)的圖像是斜率為
(π,2π]時,y=f(x)的圖像是斜率為![]() 且在y軸上的截距為-2的直線在相應區間上的部分.(1)求f(-2π)、f(-
且在y軸上的截距為-2的直線在相應區間上的部分.(1)求f(-2π)、f(-![]() )的值;(2)寫出函數y=(x)的表達式,作出其圖像,并根據圖像寫出函數的單調區間.
)的值;(2)寫出函數y=(x)的表達式,作出其圖像,并根據圖像寫出函數的單調區間.
查看答案和解析>>
科目:高中數學 來源:重難點手冊 高中數學·必修4(配人教A版新課標) 人教A版新課標 題型:044
已知函數f(x)=Asin(![]() x+
x+![]() )
)![]() 的圖象在y軸上的截距為1,它在y軸右側的第一個最大值點和最小值點分別為(x0,2)和(x0+3π,-2).
的圖象在y軸上的截距為1,它在y軸右側的第一個最大值點和最小值點分別為(x0,2)和(x0+3π,-2).
(1)求f(x)的解析式;
(2)將y=f(x)圖象上所有點的橫坐標縮短到原來的![]() 倍(縱坐標不變),然后再將所得圖象向x軸正方向平移
倍(縱坐標不變),然后再將所得圖象向x軸正方向平移![]() 個單位,得到函數y=g(x)的圖象.寫出函數y=g(x)的解析式并用列表作圖的方法畫y=g(x)在長度為一個周期的閉區間上的圖象.
個單位,得到函數y=g(x)的圖象.寫出函數y=g(x)的解析式并用列表作圖的方法畫y=g(x)在長度為一個周期的閉區間上的圖象.
查看答案和解析>>
科目:高中數學 來源:2014屆江蘇省淮安市高一下學期第一次學情調查數學(解析版) 題型:解答題
已知 =(2asin2x,a),
=(2asin2x,a),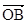 =(-1,2
=(-1,2 sinxcosx+1),O為坐標原點,a≠0,設f(x)=
sinxcosx+1),O為坐標原點,a≠0,設f(x)= ·
·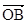 +b,b>a。
+b,b>a。
(1)若a>0,寫出函數y=f(x)的單調遞增區間;
(2)若函數y=f(x)的定義域為[ ,π],值域為[2,5],求實數a與b的值。
,π],值域為[2,5],求實數a與b的值。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com