(本小題滿分12分)
橢圓
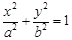
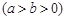
過點
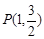
,其左、右焦點分別為
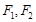
,離心率
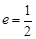
,
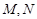
是直線
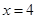
上的兩個動點,且
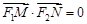
.
(1)求橢圓的方程; (2)求
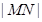
的最小值;
(3)以
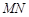
為直徑的圓
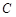
是否過定點?請證明你的結(jié)論.
解:(1)
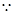
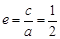
,且過點
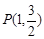
,
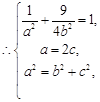
解得
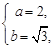
橢圓方程為

.…………4分

設(shè)點
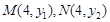
則

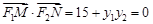
,
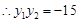
, 又
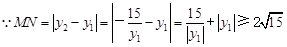
,
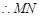
的最小值為
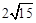
.……………………… 7分
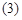
圓心
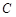
的坐標(biāo)為
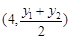
,半徑

.
圓
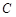
的方程為
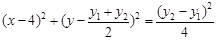
,
整理得:
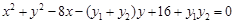
. …………10分

,
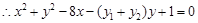
令
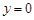
,得

,
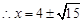
.
圓
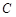
過定點
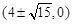
.………………12分
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
橢圓
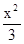
+
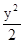
=1與橢圓
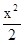
+
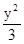
=l(l>0)有 ( )
| A.相等的焦距 | B.相同的離心率 | C.相同的準(zhǔn)線 | D.以上都不對 |
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
(本小題滿分12分).
如圖,已知某橢圓的焦點是
F1(-4,0)、
F2(4,0),過點
F2并垂直于
x軸的直線與橢圓的一個交點為
B,且|
F1B|+|
F2B|=10,橢圓上不同的兩點
A(
x1,
y1),
C(
x2,
y2)滿足條件:|
F2A|、|
F2B|、|
F2C|成等差數(shù)列.
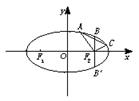
(1)求該弦橢圓的方程;
(2)求弦
AC中點的橫坐標(biāo);
(3)設(shè)弦
AC的垂直平分線的方程為
y=
kx+
m,求
m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
若橢圓
C1:
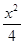
+
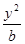
=1(0<
b<2)的離心率等于
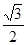
,拋物線
C2:
x2=2
py(
p>0)的焦點在橢圓
C1的頂點上.
(Ⅰ)求拋物線
C2的方程;
(Ⅱ)若過
M(-1,0)的直線
l與拋物線
C2交于
E、
F兩點,又過
E、
F作拋物線
C2的切線
l1、
l2,當(dāng)
l1⊥
l2時,求直線
l的方程.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
(本小題滿分15分)已知橢圓

的左焦點

是長軸的一個四等分點,點A、B分別為橢圓的左、右頂點,過點F且不與y軸垂直的直線

交橢圓于C、D兩點,記直線AD、BC的斜率分別為

(1)當(dāng)點D到兩焦點的距離之和為4,直線

軸時,求

的值;
(2)求

的值。
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
若點(x,y)在橢圓
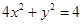
上,則
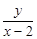
的最小值為( )
| A.1 | B.-1 | C.-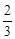  | D.以上都不對 |
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
已知橢圓
x2+(
m+3)
y2=
m(
m>0)的離心率
e=
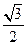
,求
m的值及橢圓的長軸和短軸的長及頂點坐標(biāo).
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
橢圓
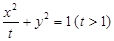
上一焦點與短軸兩端點形成的三角形的面積為1,則

.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
已知橢圓
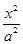
+
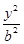
=1(a>b>0)的左焦點為F,右頂點為A,點B在橢圓上,且BF⊥x軸,直線AB交y軸于點P.若
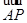
=2
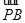
,則橢圓的離心率是( )
查看答案和解析>>

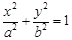
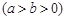 過點
過點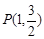 ,其左、右焦點分別為
,其左、右焦點分別為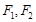 ,離心率
,離心率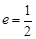 ,
,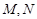 是直線
是直線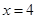 上的兩個動點,且
上的兩個動點,且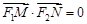 .
.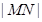 的最小值;
的最小值;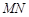 為直徑的圓
為直徑的圓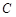 是否過定點?請證明你的結(jié)論.
是否過定點?請證明你的結(jié)論.
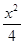 +
+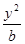 =1(0<b<2)的離心率等于
=1(0<b<2)的離心率等于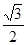 ,拋物線C2:x2=2py(p>0)的焦點在橢圓C1的頂點上.
,拋物線C2:x2=2py(p>0)的焦點在橢圓C1的頂點上. 的左焦點
的左焦點 是長軸的一個四等分點,點A、B分別為橢圓的左、右頂點,過點F且不與y軸垂直的直線
是長軸的一個四等分點,點A、B分別為橢圓的左、右頂點,過點F且不與y軸垂直的直線 交橢圓于C、D兩點,記直線AD、BC的斜率分別為
交橢圓于C、D兩點,記直線AD、BC的斜率分別為
 軸時,求
軸時,求 的值;
的值; 的值。
的值。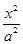 +
+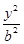 =1(a>b>0)的左焦點為F,右頂點為A,點B在橢圓上,且BF⊥x軸,直線AB交y軸于點P.若
=1(a>b>0)的左焦點為F,右頂點為A,點B在橢圓上,且BF⊥x軸,直線AB交y軸于點P.若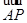 =2
=2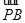 ,則橢圓的離心率是( )
,則橢圓的離心率是( )


