
【題目】已知函數![]() .
.
(1)求![]() 的單調區間;
的單調區間;
(2)如果當![]() ,且
,且![]() 時,
時,![]() 恒成立,求實數
恒成立,求實數![]() 的范圍.
的范圍.
【答案】(1)![]() 的單調遞增區間
的單調遞增區間![]() 和
和![]() ;
;![]() 的單調遞減區間
的單調遞減區間![]() .
.
(2)實數![]() 的取值范圍是
的取值范圍是![]() .
.
【解析】分析:(1)求出函數的導數,對![]() 分
分![]() 和
和![]() 兩種情況討論,即可得到函數的單調性;
兩種情況討論,即可得到函數的單調性;
(2)由題意把式子![]() 化為
化為![]() ,設
,設![]() ,
,
由(1)的結論,即可求解實數![]() 的取值范圍;或把
的取值范圍;或把![]() 可化為
可化為![]() ,設
,設![]() ,求得
,求得![]() 得出函數的單調性,令洛必達法則求解.
得出函數的單調性,令洛必達法則求解.
詳解:(1)定義域為![]() ,
,![]() ,
,
設![]() ,
,![]() ,
,
①當![]() 時,對稱軸
時,對稱軸![]() ,
,![]() ,所以
,所以![]() ,
,![]() 在
在![]() 上是增函數,
上是增函數,
②當![]() 時,
時,![]() ,所以
,所以![]() ,
,![]() 在
在![]() 上是增函數,
上是增函數,
③當![]() 時,令
時,令![]() 得
得![]() ,
,![]() ,
,
令![]() ,解得
,解得![]() ,
,![]() ;令
;令![]() ,解得
,解得![]() ,
,
所以![]() 的單調遞增區間
的單調遞增區間![]() 和
和![]() ;
;![]() 的單調遞減區間
的單調遞減區間![]() .
.
(2)![]() 可化為
可化為![]() ,設
,設![]() ,
,
由(1)知:
①當![]() 時,
時,![]() 在
在![]() 上是增函數,若
上是增函數,若![]() 時,
時,![]() ;
;
所以![]() ,
,
若![]() 時,
時,![]() ,所以
,所以![]() ,所以,當
,所以,當![]() 時,
時,![]() 式成立.
式成立.
②當![]() 時,
時,![]() 在
在![]() 是減函數,所以
是減函數,所以![]() 式不成立,
式不成立,
綜上,實數![]() 的取值范圍是
的取值范圍是![]() .
.
解法二:![]() 可化為
可化為![]() ,設
,設
![]() ,
,![]() ,
,
令![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ;
;![]() ,
,![]() ;
;
![]() ,
,![]() 在
在![]() 上,又
上,又![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ;
;
所以![]() ,
,![]() ;
;![]() ,
,![]() ;
;![]() 在
在![]() ,
,![]() ,
,
由洛必達法則![]()
![]() ,所以
,所以![]() .
.


科目:高中數學 來源: 題型:
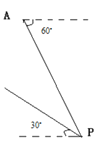
【題目】據監測,在海濱某城市附近的海面有一臺風. 臺風中心位于城市![]() 的東偏南
的東偏南![]() 方向、距離城市
方向、距離城市![]() 的海面
的海面![]() 處,并以
處,并以![]() 的速度向西偏北
的速度向西偏北![]() 方向移動(如圖示).如果臺風侵襲范圍為圓形區域,半徑
方向移動(如圖示).如果臺風侵襲范圍為圓形區域,半徑![]() ,臺風移動的方向與速度不變,那么該城市受臺風侵襲的時長為_____ .
,臺風移動的方向與速度不變,那么該城市受臺風侵襲的時長為_____ .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從甲地到乙地要經過3個十字路口,設各路口信號燈工作相互獨立,且在各路口遇到紅燈的概率分別為![]() .
.
(Ⅰ)設![]() 表示一輛車從甲地到乙地遇到紅燈的個數,求隨機變量
表示一輛車從甲地到乙地遇到紅燈的個數,求隨機變量![]() 的分布列和數學期望;
的分布列和數學期望;
(Ⅱ)若有2輛車獨立地從甲地到乙地,求這2輛車共遇到1個紅燈的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題中,正確的命題的序號為__________.
①已知隨機變量服從二項分布![]() ,若
,若![]() ,
,![]() ,則
,則![]() ;
;
②將一組數據中的每個數據都加上同一個常數后,方差恒不變;
③設隨機變量![]() 服從正態分布
服從正態分布![]() ,若
,若![]() ,則
,則![]() ;
;
④某人在![]() 次射擊中,擊中目標的次數為
次射擊中,擊中目標的次數為![]() ,
,![]() ,則當
,則當![]() 時概率最大.
時概率最大.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某家具廠有方木料90 ![]() ,五合板600
,五合板600![]() ,準備加工成書桌和書櫥出售.已知生產每張書桌需要方木料0.1
,準備加工成書桌和書櫥出售.已知生產每張書桌需要方木料0.1 ![]() ,五合板2
,五合板2 ![]() ,生產每個書櫥需要方木料0.2
,生產每個書櫥需要方木料0.2![]() ,五合板1
,五合板1 ![]() ,出售一張書桌可獲利潤80元,出售一個書櫥可獲利潤120元.請問怎樣安排生產可使所得利潤最大?
,出售一張書桌可獲利潤80元,出售一個書櫥可獲利潤120元.請問怎樣安排生產可使所得利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設某大學的女生體重y(單位:kg)與身高x(單位:cm)具有線性相關關系,根據一組樣本數據(xi,yi)(i=1,2,…,n),用最小二乘法建立的回歸方程為![]() =0.85x-85.71,則下列結論中不正確的是
=0.85x-85.71,則下列結論中不正確的是
A. y與x具有正的線性相關關系
B. 回歸直線過樣本點的中心(![]() ,
,![]() )
)
C. 若該大學某女生身高增加1cm,則其體重約增加0.85kg
D. 若該大學某女生身高為170cm,則可斷定其體重比為58.79kg
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2002年北京國際數學家大會會標,是以中國古代數學家趙爽的弦圖為基礎而設計的,弦圖用四個全等的直角三角形與一個小正方形拼成的一個大正方形![]() 如圖
如圖![]() ,若大、小正方形的面積分別為25和1,直角三角形中較大銳角為
,若大、小正方形的面積分別為25和1,直角三角形中較大銳角為![]() ,則
,則![]() 等于
等于![]()
![]()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=cosx(sinx+cosx)﹣ ![]() .
.
(1)若0<α< ![]() ,且sinα=
,且sinα= ![]() ,求f(α)的值;
,求f(α)的值;
(2)求函數f(x)的最小正周期及單調遞增區間.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com