
| A. | (0,2] | B. | [$\frac{1}{2}$,+∞) | C. | [$\frac{1}{2}$,2] | D. | [$\frac{1}{2}$,2]∪[4,+∞) |
分析 若區間[1,2]為函數f(x)=|2x-t|的“不動區間”,則函數f(x)=|2x-t|和函數F(x)=|2-x-t|在[1,2]上單調性相同,則(2x-t)(2-x-t)≤0在[1,2]上恒成立,進而得到答案.
解答 解:∵函數y=f(x)與y=F(x)的圖象關于y軸對稱,
∴F(x)=f(-x)=|2-x-t|,
∵區間[1,2]為函數f(x)=|2x-t|的“不動區間”,
∴函數f(x)=|2x-t|和函數F(x)=|2-x-t|在[1,2]上單調性相同,
∵y=2x-t和函數y=2-x-t的單調性相反,
∴(2x-t)(2-x-t)≤0在[1,2]上恒成立,
即1-t(2x+2-x)+t2≤0在[1,2]上恒成立,
即2-x≤t≤2x在[1,2]上恒成立,
即$\frac{1}{2}$≤t≤2,
故選:C
點評 本題考查的知識點是函數恒成立問題,指數函數的圖象和性質,正確理解不動區間的定義,是解答的關鍵.


 名校名師培優作業本加核心試卷系列答案
名校名師培優作業本加核心試卷系列答案 全程金卷系列答案
全程金卷系列答案科目:高中數學 來源: 題型:選擇題
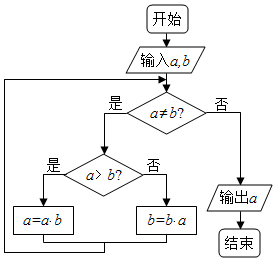 如圖程序框圖的算法思路源于我國古代數學名著《九章算術》中的“更相減損術”,執行該程序框圖,若輸入a,b分別為2,8,則輸出的a等于( )
如圖程序框圖的算法思路源于我國古代數學名著《九章算術》中的“更相減損術”,執行該程序框圖,若輸入a,b分別為2,8,則輸出的a等于( )| A. | 4 | B. | 0 | C. | 14 | D. | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1種 | B. | 2種 | C. | 3種 | D. | 4種 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -2 | B. | 2 | C. | -1 | D. | 1 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2米/秒 | B. | 3米/秒 | C. | 4米/秒 | D. | 5米/秒 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (1,4) | B. | $[\frac{5}{2},4)$ | C. | $(1,\frac{5}{2}]$ | D. | $[\frac{5}{2},\frac{8}{3}]$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com