
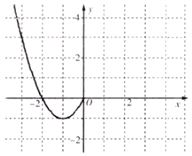
 已知函數f(x)是定義在R上的偶函數,且當x≤0時,f(x)=x2+2x.現已畫出函數f(x)在y軸左側的圖象,如圖所示,根據圖象:
已知函數f(x)是定義在R上的偶函數,且當x≤0時,f(x)=x2+2x.現已畫出函數f(x)在y軸左側的圖象,如圖所示,根據圖象:分析 (1)根據偶函數的圖象關于y軸對稱,可作出f(x)的圖象,由圖象可得f(x)的單調遞增區間;
(2)令x>0,則-x<0,根據條件可得f(-x)=x2-2x,利用函數f(x)是定義在R上的偶函數,可得f(x)=f(-x)=x2-2x,從而可得函數f(x)的解析式;
(3)先求出拋物線對稱軸x=2a--1,然后分當2a+1≤1時,當1<2a+1≤2時,當2a+1>2時三種情況,根據二次函數的增減性解答.
解答 解:(1)如圖,根據偶函數的圖象關于y軸對稱,可作出f(x)的圖象,(2分),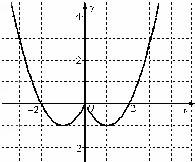
則f(x)的單調遞增區間為(-1,0),(1,+∞);(5分)
(2)令x>0,則-x<0,∴f(-x)=x2-2x
∵函數f(x)是定義在R上的偶函數,
∴f(x)=f(-x)=x2-2x
∴解析式為f(x)=$\left\{\begin{array}{l}{{x}^{2}+2x,x≤0}\\{{x}^{2}-2x,x>0}\end{array}\right.$(10分)
(3)g(x)=x2-2x-4ax+2,對稱軸為x=2a+1,
當2a+1≤1時,g(1)=1-4a為最小;
當1<2a+1≤3時,g(2a+1)=-4a2-4a+1為最小;
當2a+1>3時,g(3)=5-12a為最小;
∴g(x)min=$\left\{\begin{array}{l}{1-4a,a≤0}\\{-4{a}^{2}-4a+1,0<a<1}\\{5-12a,a≥1}\end{array}\right.$.(16分)
點評 本題考查函數圖象的作法,考查函數解析式的確定與函數的單調性,考查學生分析解決問題的能力,屬于中檔題.


 輕巧奪冠周測月考直通中考系列答案
輕巧奪冠周測月考直通中考系列答案科目:高中數學 來源: 題型:選擇題
| A. | 11 | B. | 12 | C. | 13 | D. | 不能確定 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 命題p:?α∈R,使冪函數y=xα圖象經過第四象限;命題q:在銳角△ABC中,sinA>cosB,則p∧q為真 | |
| B. | 命題:“正切函數y=tan x在定義域內為增函數”的逆否命題為真 | |
| C. | 在區間(a,b)連續的函數f(x),f(a)•f(b)<0是f(x)在區間(a,b)內有零點的充要條件 | |
| D. | 命題p:函數f(x)=x2-2x僅有兩個零點,則?p是真命題 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com