
【題目】設![]() ,
,![]()
(1)求![]() 在區間
在區間![]() 上的值域;
上的值域;
(2)求![]() 在區間
在區間![]() 上的值域:
上的值域:
(3)已知![]() ,若對于任意
,若對于任意![]() ,總存在
,總存在![]() ,使得
,使得![]() 成立,求
成立,求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() (2)見詳解 (3)
(2)見詳解 (3)![]()
【解析】
(1) 根據題意,判斷出![]() 在
在![]() 上的單調性,即可求出
上的單調性,即可求出![]() 在區間
在區間![]() 上的值域;
上的值域;
(2) 根據題意,先求出![]() 的對稱軸,再根據區間
的對稱軸,再根據區間![]() 與對稱軸的位置關系進行分類討論,即可求出
與對稱軸的位置關系進行分類討論,即可求出![]() 在區間
在區間![]() 上的值域;
上的值域;
(3) 根據題意,只需滿足![]() 在區間
在區間![]() 上的值域是
上的值域是![]() 在區間
在區間![]() 上的值域的子集,根據集合之間的包含關系即可求得
上的值域的子集,根據集合之間的包含關系即可求得![]() 的取值范圍。
的取值范圍。
(1) 根據題意,可得![]()
易知![]() 在
在![]() 上是單調遞增的,
上是單調遞增的,
![]()
![]()
![]() 在區間
在區間![]() 上的值域為
上的值域為![]() .
.
(2)由題意得,![]() 的對稱軸為
的對稱軸為![]() ,則
,則
當![]() 時,
時,![]() 在區間
在區間![]() 上單調遞增,
上單調遞增,
![]() ,
,![]() 在區間
在區間![]() 上的值域為
上的值域為![]() ;
;
當![]() 時,
時,![]() 在區間
在區間![]() 上單調遞減,
上單調遞減,
![]() ,
,![]() 在區間
在區間![]() 上的值域為
上的值域為![]() ;
;
當![]() 時,
時,![]() 在區間
在區間![]() 上先減后增,
上先減后增,
![]()
若![]() ,則
,則 ![]() ,
,![]() 在區間
在區間![]() 上的值域為
上的值域為![]() ;
;
若![]() ,則
,則 ![]() ,
,![]() 在區間
在區間![]() 上的值域為
上的值域為![]() ;
;
若![]() ,則
,則 ![]() ,
,![]() 在區間
在區間![]() 上的值域為
上的值域為![]() ;
;
(3) 根據(1)(2)可知,![]() 在區間
在區間![]() 上的值域為
上的值域為![]() ,當
,當![]() 時,
時,![]() 在區間
在區間![]() 上的值域為
上的值域為![]() ;若對于任意
;若對于任意![]() ,總存在
,總存在![]() ,使得
,使得![]() 成立,只需滿足
成立,只需滿足![]() 在區間
在區間![]() 上的值域是
上的值域是![]() 在區間
在區間![]() 上的值域的子集,即
上的值域的子集,即

解得![]()


科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,C為直線y=5上的動點,以C為圓心的圓C截y軸所得的弦長恒為6,過原點O作圓C的一條切線,切點為P,則點P到直線3x+4y﹣25=0的距離的最小值為_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() 與直線
與直線![]() ,動直線
,動直線![]() 過定點
過定點![]() .
.
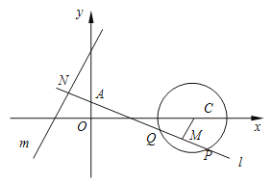
(1)若直線![]() 與圓
與圓![]() 相切,求直線
相切,求直線![]() 的方程;
的方程;
(2)若直線![]() 與圓
與圓![]() 相交于
相交于![]() 兩點,點
兩點,點![]() 是
是![]() 的中點,直線
的中點,直線![]() 與直線
與直線![]() 相交于點
相交于點![]() . 探索
. 探索![]() 是否為定值,若是,求出該定值;若不是,請說明理由.
是否為定值,若是,求出該定值;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】商店出售茶壺和茶杯,茶壺定價每個20元,茶杯每個5元,該商店推出兩種優惠辦法:(1)買一個茶壺贈一個茶杯;(2)按總價的92%付款.
某顧客需購買茶壺4個,茶杯若干個(不少于4個),若購買茶杯數x個,付款y(元),分別建立兩種優惠辦法中y與x之間的函數關系式,并討論該顧客買同樣多的茶杯時,兩種辦法哪一種更優惠。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校高三有500名學生,在一次考試的英語成績服從正態分布![]() ,數學成績的頻率分布直方圖如下:
,數學成績的頻率分布直方圖如下:
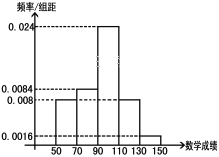
(Ⅰ)如果成績大于135的為特別優秀,則本次考試英語、數學特別優秀的大約各多少人?
(Ⅱ)試問本次考試英語和數學的成績哪個較高,并說明理由.
(Ⅲ)如果英語和數學兩科都特別優秀的共有6人,從(Ⅰ)中的這些同學中隨機抽取3人,設三人中兩科都特別優秀的有![]() 人,求
人,求![]() 的分布列和數學期望。
的分布列和數學期望。
參考公式及數據:
若![]() ,則
,則![]() ,
,
![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】抽樣得到某次考試中高二年級某班![]() 名學生的數學成績和物理成績如下表:
名學生的數學成績和物理成績如下表:
學生編號 |
|
|
|
|
|
|
數學成績 |
|
|
|
|
|
|
物里成績 |
|
|
|
|
|
|
(1)在圖中畫出表中數據的散點圖;
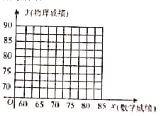
(2)建立![]() 關于
關于![]() 的回歸方程:(系數保留到小數點后兩位).
的回歸方程:(系數保留到小數點后兩位).
(3)如果某學生的數學成績為![]() 分,預測他本次的物理成績(成績取整數).
分,預測他本次的物理成績(成績取整數).
參考公式:回歸方程為![]() ,其中
,其中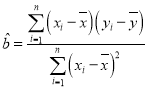 ,
,![]() .
.
參考數據:![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《中國青年報》2015年5月14日報道:“伴隨著網絡技術的蓬勃發展,國內電子商務獲得了爆炸式的增長,2014年網上零售額達到了27898億元,占社會消費品零售總額的10%,也就是說,人們日常消費中10%是通過網購,而且還以年30%,40%的速度增長."假設2014-2020年網上零售額每年的增長率均為35%,試算出2015-2020年每年的網上零售額(精確到1億元).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某商場在促銷期間規定:商場內所有商品按標價的![]() 出售,當顧客在商場內消費一定金額后,按如下方案獲得相應金額的獎券:
出售,當顧客在商場內消費一定金額后,按如下方案獲得相應金額的獎券:
消費金額(元)的范圍 |
|
|
|
| … |
獲得獎券的金額(元) | 30 | 60 | 100 | 130 | … |
根據上述促銷方法,顧客在該商場購物可以獲得雙重優惠,例如:購買標價為400元的商品,則消費金額為320元,獲得的優惠額為:![]() 元,設購買商品得到的優惠率=(購買商品獲得的優惠額)/(商品標價),試問:
元,設購買商品得到的優惠率=(購買商品獲得的優惠額)/(商品標價),試問:
(1)若購買一件標價為1000元的商品,顧客得到的優惠率是多少?
(2)對于標價在![]() (元)內的商品,顧客購買標價為多少元的商品,可得到不小于
(元)內的商品,顧客購買標價為多少元的商品,可得到不小于![]() 的優惠率?
的優惠率?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,在△![]() 中,
中,![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點,
的中點,![]() 為
為![]() 的中點,
的中點,![]() ,
,![]() .將△
.將△![]() 沿
沿![]() 折起到△
折起到△![]() 的位置,使得平面
的位置,使得平面![]() 平面
平面![]() ,如圖2.
,如圖2.
(Ⅰ)求證:![]() ;
;
(Ⅱ)求直線![]() 和平面
和平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)線段![]() 上是否存在點
上是否存在點![]() ,使得直線
,使得直線![]() 和
和![]() 所成角的余弦值為
所成角的余弦值為![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.

圖1 圖2
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com