
分析 (1)觀察已知排列的數,依次正整數的個數是,1,2,4,8,…,分析得出是規律,根據規律求出第n行的最后一個數.
(2)由(1)得到第n行的第一個數,且此行一共有2 n-1個數,從而利用等差數列的求和公式即可計算第n行的各個數之和;
(3)由(1)可知第n行的最后一個數是2n-1,即可推斷
(4)對于存在性問題,可先假設存在,即存在n使得S′=227-213-120,再利用(II)的結論,構建等式,若出現矛盾,則說明假設不成立,即不存在;否則存在.
解答 解:(1)由已知得出每行的正整數的個數是1,2,4,8,…,其規律:
1=21-1,
2=22-1,
4=23-1,
8=24-1,
…,
由此得出第n行的第一個數為:2n-1,共有2n-1個,
所以此表第n行的最后一個數是2n-1
(2)由(1)得到第n行的第一個數,且此行一共有2 n-1個數,從而利用等差數列的求和公式得:
第n行的各個數之和S=$\frac{{2}^{n-1}({2}^{n-1}+{2}^{n}-1)}{2}$=$\frac{3}{8}$•4n-$\frac{1}{4}$•2n=3×22n-3-2n-2,
(3)由(1)可知第n行的最后一個數是2n-1,
當n=11時,最后一個數字為1023,
當n=12時,最后一個數字為2047,
所以2010在第第12行,2010-1023=987,
故2010是第12行的第987個數;
(III)第n行起的連續10行的所有數之和S=$\frac{3}{8}$•4n(1+4+…+49)-$\frac{1}{4}$•2n=(1+2+…+29)
=2n-2(2n+19-2n-1-1023),
又227-213-120=23(224-210-15)
若存在n使得S′=227-213-120,
則2n-2(2n+19-2n-1-1023)=23(224-210-15)…(*)
所以n-2≥3,所以n≥5.n=5時,(*)式成立,
n>5時由(*)可得2n-5(2n+19-2n-1-1023)=224-210-15,
此等式左邊偶數右邊奇數,不成立.
所以滿足條件的n=5.
點評 此題考查的知識點是等差數列與等比數列的綜合、圖形數字的變化類問題,同時考查學生分析歸納問題的能力,其關鍵是從每行的正整數個數1,2,4,8,…這列數找出規律解答.


科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{5}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | b-a<b-c | B. | logab>logcb | C. | ab+cb<(a+c)b | D. | loga(c-b)>logc(a-b) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 常 喝 | 不常喝 | 總 計 | |
| 肥 胖 | 2 | ||
| 不肥胖 | 18 | ||
| 總 計 | 30 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
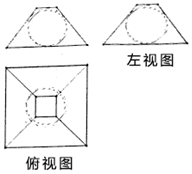 如圖是某幾何體挖去一部分后得到的三視圖,其中主視圖和左視圖相同都是一個等腰梯形及它的內切圓,俯視圖中有兩個邊長分別為2和8的正方形且圖中的圓與主視圖圓大小相等并且圓心為兩個正方形的中心.問該幾何體的體積是( )
如圖是某幾何體挖去一部分后得到的三視圖,其中主視圖和左視圖相同都是一個等腰梯形及它的內切圓,俯視圖中有兩個邊長分別為2和8的正方形且圖中的圓與主視圖圓大小相等并且圓心為兩個正方形的中心.問該幾何體的體積是( )| A. | $\frac{420-32π}{3}$ | B. | $\frac{336-32π}{3}$ | C. | $\frac{168-4π}{3}$ | D. | $\frac{168\sqrt{2}-64\sqrt{2}π}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 推理的形式錯誤 | B. | 大前提是錯誤的 | C. | 小前提是錯誤的 | D. | 結論是正確的 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com