
分析 (Ⅰ)根據概率的乘法公式,求出對應的概率,即可得到結論.
(Ⅱ)利用離散型隨機變量分別求出對應的概率,即可求X的分布列;以及數學期望.
解答 解:(I)用A表示甲在4局以內(含4局)贏得比賽的是事件,Ak表示第k局甲獲勝,Bk表示第k局乙獲勝,
則P(Ak)=$\frac{2}{3}$,P(Bk)=$\frac{1}{3}$,k=1,2,3,4,5
P(A)=P(A1A2)+P(B1A2A3)+P(A1B2A3A4)=($\frac{2}{3}$)2+$\frac{1}{3}×$($\frac{2}{3}$)2+$\frac{2}{3}$×$\frac{1}{3}$×($\frac{2}{3}$)2=$\frac{56}{81}$.
(Ⅱ)X的可能取值為2,3,4,5.
P(X=2)=P(A1A2)+P(B1B2)=$\frac{5}{9}$,
P(X=3)=P(B1A2A3)+P(A1B2B3)=$\frac{2}{9}$,
P(X=4)=P(A1B2A3A4)+P(B1A2B3B4)=$\frac{10}{81}$,
P(X=5)=P(A1B2A3B4A5)+P(B1A2B3A4B5)+P(B1A2B3A4A5)+P(A1B2A3B4B5)=$\frac{8}{81}$,
或者P(X=5)=1-P(X=2)-P(X=3)-P(X=4)=$\frac{8}{81}$,
故分布列為:
| X | 2 | 3 | 4 | 5 |
| P | $\frac{5}{9}$ | $\frac{2}{9}$ | $\frac{10}{81}$ | $\frac{8}{81}$ |
點評 本題考查了相互獨立事件、互斥事件的概率計算公式、隨機變量的分布列與數學期望,考查了推理能力與計算能力,屬于中檔題.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $3\sqrt{3}$ | B. | $2\sqrt{6}$ | C. | $\sqrt{21}$ | D. | $2\sqrt{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 停車距離d(米) | (10,20] | (20,30] | (30,40] | (40,50] | (50,60] |
| 頻數 | 26 | a | b | 8 | 2 |
| 平均每毫升血液酒精含量x毫克 | 10 | 30 | 50 | 70 | 90 |
| 平均停車距離y米 | 30 | 50 | 60 | 70 | 90 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
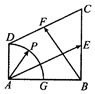 在直角梯形ABCD中,AB⊥AD,AD∥BC,AB=BC=2AD=2,E,F分別為BC,CD的中點,以A為圓心,AD為半徑的圓交AB于G,點P在$\widehat{DG}$上運動(如圖).若$\overrightarrow{AP}$=λ$\overrightarrow{AE}$+μ$\overrightarrow{BF}$,其中λ,μ∈R,則6λ+μ的取值范圍是( )
在直角梯形ABCD中,AB⊥AD,AD∥BC,AB=BC=2AD=2,E,F分別為BC,CD的中點,以A為圓心,AD為半徑的圓交AB于G,點P在$\widehat{DG}$上運動(如圖).若$\overrightarrow{AP}$=λ$\overrightarrow{AE}$+μ$\overrightarrow{BF}$,其中λ,μ∈R,則6λ+μ的取值范圍是( )| A. | [1,$\sqrt{2}$] | B. | [$\sqrt{2}$,2$\sqrt{2}$] | C. | [2,2$\sqrt{2}$] | D. | [1,2$\sqrt{2}$] |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
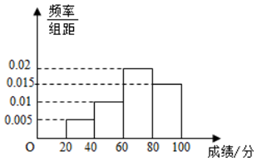 隨著社會的發展,食品安全問題漸漸成為社會關注的熱點,為了提高學生的食品安全意識,某學校組織全校學生參加食品安全知識競賽,成績的頻率分布直方圖如圖所示,數據的分組依次為[20,40),[40,60),[60,80),[80,100),若該校的學生總人數為3000,則成績不超過60分的學生人數大約為900.
隨著社會的發展,食品安全問題漸漸成為社會關注的熱點,為了提高學生的食品安全意識,某學校組織全校學生參加食品安全知識競賽,成績的頻率分布直方圖如圖所示,數據的分組依次為[20,40),[40,60),[60,80),[80,100),若該校的學生總人數為3000,則成績不超過60分的學生人數大約為900.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,e) | B. | (1,+∞) | C. | (1,e) | D. | (e,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
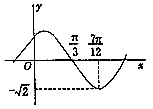 (1)求f(x)=tan(3x-$\frac{π}{4}$)的定義域;
(1)求f(x)=tan(3x-$\frac{π}{4}$)的定義域;查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com