
【題目】已知函數![]() .
.
(1)![]() 時,求
時,求![]() 在
在![]() 上的單調區間;
上的單調區間;
(2)![]() 且
且![]() ,
, ![]() 均恒成立,求實數
均恒成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1) ![]() 的單調增區間是
的單調增區間是![]() ,單調減區間是
,單調減區間是![]() ;(2)
;(2) ![]() .
.
【解析】試題分析:(1)求出![]() ,令
,令![]() 在
在![]() 內求得
內求得![]() 的范圍,可得函數
的范圍,可得函數![]() 增區間,令
增區間,令![]() 在
在![]() 內求得
內求得![]() 的范圍,可得函數
的范圍,可得函數![]() 的減區間;(2)
的減區間;(2)![]() 時,
時, ![]() ,即
,即![]() ;
; ![]() 時,
時, ![]() ,即
,即![]() , 設
, 設![]() ,分兩種情況研究函數的單調性,并求出
,分兩種情況研究函數的單調性,并求出![]() 的最值,從而可得實數
的最值,從而可得實數![]() 的取值范圍.
的取值范圍.
試題解析:(1)![]() 時,
時, ![]() ,設
,設![]() ,
,
當![]() 時,
時, ![]() ,則
,則![]() 在
在![]() 上是單調遞減函數,即則
上是單調遞減函數,即則![]() 在
在![]() 上是單調遞減函數,
上是單調遞減函數,
∵![]() ∴
∴![]() 時,
時, ![]() ;
; ![]() 時,
時, ![]()
∴在![]() 上
上![]() 的單調增區間是
的單調增區間是![]() ,單調減區間是
,單調減區間是![]() ;
;
(2)![]() 時,
時, ![]() ,即
,即![]() ;
;
![]() 時,
時, ![]() ,即
,即![]() ;
;
設![]()
則![]()
![]() 時,
時, ![]() ,∵
,∵![]() ,∴
,∴ ![]() 在
在![]() 上單調遞增
上單調遞增
∴![]() 時,
時, ![]() ;
; ![]() 時,
時, ![]() ,∴
,∴ ![]() 符合題意;
符合題意;
![]() 時,
時, ![]() ,
, ![]() 時,
時, ![]() ,∴
,∴ ![]() 在
在![]() 上單調遞減,
上單調遞減,
∴當![]() 時,
時, ![]() ,與
,與![]() 時,
時, ![]() 矛盾;舍
矛盾;舍
![]() 時,設
時,設![]() 為
為![]() 和0中的最大值,當
和0中的最大值,當![]() 時,
時, ![]() ,
,
∴![]() 在
在![]() 上單調遞減,∴當
上單調遞減,∴當![]() 時,
時, ![]() ,與
,與![]() 時,
時, ![]() 矛盾;舍
矛盾;舍
綜上, ![]()


 字詞句篇與同步作文達標系列答案
字詞句篇與同步作文達標系列答案科目:高中數學 來源: 題型:
【題目】(導學號:05856308)(12分)
如圖,∠ABC=![]() ,O為AB上一點,3OB=3OC=2AB,PO⊥平面ABC,2DA=2AO=PO,OA=1,且DA∥PO.
,O為AB上一點,3OB=3OC=2AB,PO⊥平面ABC,2DA=2AO=PO,OA=1,且DA∥PO.
(Ⅰ)求證:平面PBD⊥平面COD;
(Ⅱ)求點O到平面BDC的距離.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2018四川綿陽南山中學高三二診熱身考試】以下四個命題中:
①某地市高三理科學生有15000名,在一次調研測試中,數學成績![]() 服從正態分布
服從正態分布![]() ,已知
,已知![]() ,若按成績分層抽樣的方式抽取100分試卷進行分析,則應從120分以上(包括120分)的試卷中抽取15分;
,若按成績分層抽樣的方式抽取100分試卷進行分析,則應從120分以上(包括120分)的試卷中抽取15分;
②已知命題![]() ,
,![]() ,則
,則![]() ,
,![]() ;
;
③在![]() 上隨機取一個數
上隨機取一個數![]() ,能使函數
,能使函數![]() 在
在![]() 上有零點的概率為
上有零點的概率為![]() ;
;
④在某次飛行航程中遭遇惡劣氣候,用分層抽樣的20名男乘客中有5名暈機,12名女乘客中有8名暈機,在檢驗這些乘客暈機是否與性別有關時,采用獨立性檢驗,有97%以上的把握認為與性別有關.
| 0.15 | 0.1 | 0.05 | 0.025 |
| 2.072 | 2.706 | 3.841 | 5.024 |
其中真命題的序號為( )
A. ①②③ B. ②③④ C. ①②④ D. ①③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設命題p:關于x的二次方程x2+(a+1)x+a-2=0的一個根大于零,另一根小于零;命題q:不等式2x2+x>2+ax對x∈(-∞,-1)恒成立.如果命題“p∨q”為真命題,命題“p∧q”為假命題,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左右焦點分別為
的左右焦點分別為![]() , 若橢圓上一點
, 若橢圓上一點![]() 滿足
滿足![]() ,且橢圓
,且橢圓![]() 過點
過點![]() ,過點
,過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于兩點
交于兩點![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若點![]() 是點
是點![]() 在
在![]() 軸上的垂足,延長
軸上的垂足,延長![]() 交橢圓
交橢圓![]() 于
于![]() ,求證:
,求證: ![]() 三點共線.
三點共線.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知多面體![]() 的底面
的底面![]() 是邊長為2的正方形,
是邊長為2的正方形, ![]() 底面
底面![]() ,
, ![]() ,且
,且![]() .
.
(Ⅰ)記線段![]() 的中點為
的中點為![]() ,在平面
,在平面![]() 內過點
內過點![]() 作一條直線與平面
作一條直線與平面![]() 平行,要求保留作圖痕跡,但不要求證明.
平行,要求保留作圖痕跡,但不要求證明.
(Ⅱ)求直線![]() 與平面
與平面![]() 所成角的正弦值;
所成角的正弦值;

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“過大年,吃水餃”是我國不少地方過春節的一大習俗,2018年春節前夕,![]() 市某質檢部門隨機抽取了100包某種品牌的速凍水餃,檢測其某項質量指標.
市某質檢部門隨機抽取了100包某種品牌的速凍水餃,檢測其某項質量指標.
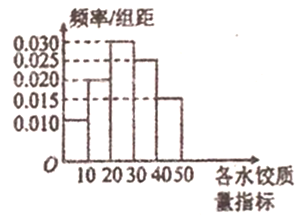
(1)求所抽取的100包速凍水餃該項質量指標值的樣本平均數![]() (同一組中的數據用該組區間的中點值作代表);
(同一組中的數據用該組區間的中點值作代表);
(2)①由直方圖可以認為,速凍水餃的該項質量指標值![]() 服從正態分布
服從正態分布![]() ,利用該正態分布,求
,利用該正態分布,求![]() 落在
落在![]() 內的概率;
內的概率;
②將頻率視為概率,若某人從某超市購買了4包這種品牌的速凍水餃,記這4包速凍水餃中這種質量指標值位于![]() 內的包數為
內的包數為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
附:①計算得所抽查的這100包速凍水餃的質量指標的標準差為![]() ;
;
②若![]() ,則
,則![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖甲,在四邊形ABCD中, ![]() ,
, ![]() 是邊長為4的正三角形,把
是邊長為4的正三角形,把![]() 沿AC折起到
沿AC折起到![]() 的位置,使得平面PAC
的位置,使得平面PAC![]() 平面ACD,如圖乙所示,點
平面ACD,如圖乙所示,點![]() 分別為棱
分別為棱![]() 的中點.
的中點.
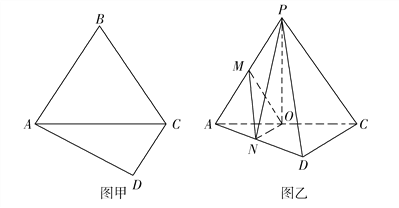
(1)求證: ![]() 平面
平面![]() ;
;
(2)求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com