
【題目】設函數![]() (a,b
(a,b![]() R)的導函數為
R)的導函數為![]() ,已知
,已知![]() ,
,![]() 是
是![]() 的兩個不同的零點.
的兩個不同的零點.
(1)證明:![]() ;
;
(2)當b=0時,若對任意x>0,不等式![]() 恒成立,求a的取值范圍;
恒成立,求a的取值范圍;
(3)求關于x的方程![]() 的實根的個數.
的實根的個數.
【答案】(1)見解析;(2)![]() ;(3)1個.
;(3)1個.
【解析】
(1)求函數的導數,利用△=4a2﹣12b>0,得證;
(2)分離參數a,所以a≥![]() ﹣x對任意x>0恒成立,令新函數設g(x)=
﹣x對任意x>0恒成立,令新函數設g(x)=![]() ﹣x求最值即可,或采用x3+ax2﹣xlnx≥0時求左側最值亦可.
﹣x求最值即可,或采用x3+ax2﹣xlnx≥0時求左側最值亦可.
(3)轉化函數求零點個數可得結論.
(1)函數f(x)=x3+ax2+bx(a,b∈R)的導函數為f′(x)=3x2+2ax+b.
已知x1,x2是f'(x)的兩個不同的零點,設x1<x2,
所以△=4a2﹣12b>0,所以:a2>3b得證;
(2)當b=0時,對任意x>0,f(x)≥xlnx恒成立,
所以x3+ax2≥xlnx,即x3+ax2﹣xlnx≥0,x2+ax﹣lnx≥0對任意x>0恒成立,
所以a≥![]() ﹣x對任意x>0恒成立,
﹣x對任意x>0恒成立,
設g(x)=![]() ﹣x,則
﹣x,則![]() ,
,
令h(x)=1﹣1nx﹣x2,則h![]() (x)=﹣
(x)=﹣![]() ﹣2x<0,
﹣2x<0,
所以h(x)在(0,+∞)上單調遞減,注意到h(1)=0,
當x∈(0,1)時,h(x)>0,g![]() (x)>0,所以g(x)在(0,1)上單調遞增,
(x)>0,所以g(x)在(0,1)上單調遞增,
當x∈(1,+∞)時,H(x)<0,g![]() (x)<0,所以g(x)在(1,+∞)上單調遞減,
(x)<0,所以g(x)在(1,+∞)上單調遞減,
所以,當x=1時,g(x)有最大值g(1)=﹣1,
所以a的取值范圍為[﹣1,+∞);
(3)由題意設F(x)=f(x)﹣f(x1)﹣![]() ,
,
則原問題轉化為求函數F(x)的零點的個數,
因為導函數為f![]() (x)=3x2+2ax+b,已知x1,x2是f'(x)的兩個不同的零點,
(x)=3x2+2ax+b,已知x1,x2是f'(x)的兩個不同的零點,
所以:![]() ,所以:
,所以:
![]() ,
,
所以F(x)在(0,+∞)上單調遞增,注意到F(x1)=0,所以F(x)在(0,+∞)上存在唯一零點x1,
∴關于x的方程![]() 有1個實根,
有1個實根,


科目:高中數學 來源: 題型:
【題目】已知某商品每件的生產成本![]() (元)與銷售價格
(元)與銷售價格![]() (元)具有線性相關關系,對應數據如表所示:
(元)具有線性相關關系,對應數據如表所示:
| 5 | 6 | 7 | 8 |
| 15 | 17 | 21 | 27 |
(1)求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(2)若該商品的月銷售量![]() (千件)與生產成本
(千件)與生產成本![]() (元)的關系為
(元)的關系為![]() ,
,![]() ,根據(1)中求出的線性回歸方程,預測當
,根據(1)中求出的線性回歸方程,預測當![]() 為何值時,該商品的月銷售額最大.
為何值時,該商品的月銷售額最大.
附: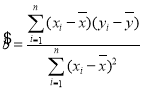 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() ,
,![]() 是長軸的一個端點,弦
是長軸的一個端點,弦![]() 過橢圓的中心
過橢圓的中心![]() ,點
,點![]() 在第一象限,且
在第一象限,且![]() ,
,![]() .
.
(1)求橢圓的標準方程;
(2)設![]() 、
、![]() 為橢圓上不重合的兩點且異于
為橢圓上不重合的兩點且異于![]() 、
、![]() ,若
,若![]() 的平分線總是垂直于
的平分線總是垂直于![]() 軸,問是否存在實數
軸,問是否存在實數![]() ,使得
,使得![]() ?若不存在,請說明理由;若存在,求
?若不存在,請說明理由;若存在,求![]() 取得最大值時的
取得最大值時的![]() 的長.
的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() :
:![]() 的焦點為
的焦點為![]() ,直線
,直線![]() 與拋物線
與拋物線![]() 交于
交于![]() ,
,![]() 兩點,
兩點,![]() 是坐標原點.
是坐標原點.
(1)若直線![]() 過點
過點![]() 且
且![]() ,求直線
,求直線![]() 的方程;
的方程;
(2)已知點![]() ,若直線
,若直線![]() 不與坐標軸垂直,且
不與坐標軸垂直,且![]() ,證明:直線
,證明:直線![]() 過定點.
過定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() (a>b>0),四點P1(1,1),P2(0,1),P3(–1,
(a>b>0),四點P1(1,1),P2(0,1),P3(–1, ![]() ),P4(1,
),P4(1, ![]() )中恰有三點在橢圓C上.
)中恰有三點在橢圓C上.
(1)求C的方程;
(2)設直線l不經過P2點且與C相交于A,B兩點.若直線P2A與直線P2B的斜率的和為–1,證明:l過定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知F是拋物線C:![]() 的焦點,過E(﹣l,0)的直線
的焦點,過E(﹣l,0)的直線![]() 與拋物線分別交于A,B兩點(點A,B在x軸的上方).
與拋物線分別交于A,B兩點(點A,B在x軸的上方).
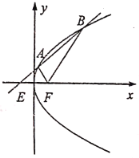
(1)設直線AF,BF的斜率分別為![]() ,
,![]() ,證明:
,證明:![]() ;
;
(2)若![]() ABF的面積為4,求直線
ABF的面積為4,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某省確定從2021年開始,高考采用“![]() ”的模式,取消文理分科,即“3”包括語文、數學、英語,為必考科目:“1”表示從物理、歷史中任選一門;“2”則是從生物、化學、地理、政治中選擇兩門,共計六門考試科目.某高中從高一年級2000名學生(其中女生900人)中,采用分層抽樣的方法抽取
”的模式,取消文理分科,即“3”包括語文、數學、英語,為必考科目:“1”表示從物理、歷史中任選一門;“2”則是從生物、化學、地理、政治中選擇兩門,共計六門考試科目.某高中從高一年級2000名學生(其中女生900人)中,采用分層抽樣的方法抽取![]() 名學生進行調查.
名學生進行調查.
(1)已知抽取的![]() 名學生中含男生110人,求
名學生中含男生110人,求![]() 的值及抽取到的女生人數;
的值及抽取到的女生人數;
(2)學校計劃在高二上學期開設選修中的“物理”和“歷史”兩個科目,為了了解學生對這兩個科目的選課情況,對在(1)的條件下抽取到的![]() 名學生講行問卷調查(假定每名學生在這兩個科目中必須選擇一個科目且只能選擇一個科目).下表是根據調查結果得到的
名學生講行問卷調查(假定每名學生在這兩個科目中必須選擇一個科目且只能選擇一個科目).下表是根據調查結果得到的![]() 列聯表,請將列聯表補充完整,并判斷是否有
列聯表,請將列聯表補充完整,并判斷是否有![]() 的把握認為選擇科目與性別有關?說明你的理由;
的把握認為選擇科目與性別有關?說明你的理由;
性別 | 選擇物理 | 選擇歷史 | 總計 |
男生 | 50 | ||
女生 | 30 | ||
總計 |
(3)在(2)的條件下,從抽取的選擇“物理”的學生中按分層抽樣抽取6人,再從這6名學生中抽取2人,對“物理”的選課意向作深入了解,求2人中至少有1名女生的概率.
參考公式:![]() ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某隧道的剖面圖是由半圓及矩形![]() 組成,交通部門擬在隧道頂部安裝通風設備(視作點
組成,交通部門擬在隧道頂部安裝通風設備(視作點![]() ),為了固定該設備,計劃除從隧道最高點
),為了固定該設備,計劃除從隧道最高點![]() 處使用鋼管垂直向下吊裝以外,再在兩側自
處使用鋼管垂直向下吊裝以外,再在兩側自![]() 兩點分別使用鋼管支撐.已知道路寬
兩點分別使用鋼管支撐.已知道路寬![]() ,設備要求安裝在半圓內部,所使用的鋼管總長度為
,設備要求安裝在半圓內部,所使用的鋼管總長度為![]() .
.
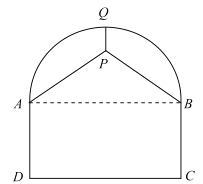
(1)①設![]() ,將
,將![]() 表示為關于
表示為關于![]() 的函數;
的函數;
②設![]() ,將
,將![]() 表示為關于
表示為關于![]() 的函數;
的函數;
(2)請選用(1)中的一個函數關系式,說明如何設計,所用的鋼管材料最省?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com