
【題目】如圖,已知F是拋物線C:![]() 的焦點,過E(﹣l,0)的直線
的焦點,過E(﹣l,0)的直線![]() 與拋物線分別交于A,B兩點(點A,B在x軸的上方).
與拋物線分別交于A,B兩點(點A,B在x軸的上方).
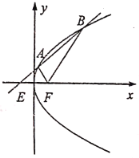
(1)設直線AF,BF的斜率分別為![]() ,
,![]() ,證明:
,證明:![]() ;
;
(2)若![]() ABF的面積為4,求直線
ABF的面積為4,求直線![]() 的方程.
的方程.
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】設函數![]() (a,b
(a,b![]() R)的導函數為
R)的導函數為![]() ,已知
,已知![]() ,
,![]() 是
是![]() 的兩個不同的零點.
的兩個不同的零點.
(1)證明:![]() ;
;
(2)當b=0時,若對任意x>0,不等式![]() 恒成立,求a的取值范圍;
恒成立,求a的取值范圍;
(3)求關于x的方程![]() 的實根的個數.
的實根的個數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某電視臺為了了解某社區居民對某娛樂節目的收視情況,隨機抽取了![]() 名觀眾進行調查,下面是根據調查結果繪制的觀眾日均收看該娛樂節目時間的頻率分布直方圖:
名觀眾進行調查,下面是根據調查結果繪制的觀眾日均收看該娛樂節目時間的頻率分布直方圖:
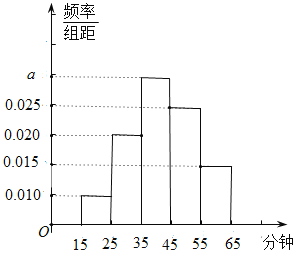
(1)求實數![]() 的值;
的值;
(2)根據統計結果,試估計觀眾觀看該娛樂節目時間的中位數(結果保留一位小數);
(3)從觀看時間在![]() ,
,![]() 的人中用分層抽樣的方法抽取6人,再從這6人中隨機抽取2人,求這2人的觀看時間都在
的人中用分層抽樣的方法抽取6人,再從這6人中隨機抽取2人,求這2人的觀看時間都在![]() 中的概率.
中的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在多面體ABCDEF中,底面ABCD是邊長為2的菱形,![]() ,四邊形BDEF是矩形,平面
,四邊形BDEF是矩形,平面![]() 平面ABCD,
平面ABCD,![]() ,H是CF的中點.
,H是CF的中點.

(1)求證:![]() 平面BDEF;
平面BDEF;
(2)求直線DH與平面CEF所成角的正弦值;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】教材曾有介紹:圓![]() 上的點
上的點![]() 處的切線方程為
處的切線方程為![]() .我們將其結論推廣:橢圓
.我們將其結論推廣:橢圓![]() (
(![]() )上的點
)上的點![]() 處的切線方程為
處的切線方程為![]() ,在解本題時可以直接應用.已知,直線
,在解本題時可以直接應用.已知,直線![]() 與橢圓
與橢圓![]() :
:![]() (
(![]() )有且只有一個公共點.
)有且只有一個公共點.
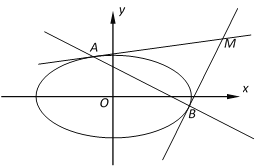
(1)求橢圓![]() 的方程;
的方程;
(2)設![]() 為坐標原點,過橢圓
為坐標原點,過橢圓![]() 上的兩點
上的兩點![]() 、
、![]() 分別作該橢圓的兩條切線
分別作該橢圓的兩條切線![]() 、
、![]() ,且
,且![]() 與
與![]() 交于點
交于點![]() .當
.當![]() 變化時,求
變化時,求![]() 面積的最大值;
面積的最大值;
(3)若![]() 是橢圓
是橢圓![]()
![]() 上不同的兩點,
上不同的兩點,![]()
![]() 軸,圓
軸,圓![]() 過
過![]() 且橢圓
且橢圓![]() 上任意一點都不在圓
上任意一點都不在圓![]() 內,則稱圓
內,則稱圓![]() 為該橢圓的一個內切圓.試問:橢圓
為該橢圓的一個內切圓.試問:橢圓![]() 是否存在過左焦點
是否存在過左焦點![]() 的內切圓?若存在,求出圓心
的內切圓?若存在,求出圓心![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合A={x|1-a≤x≤1+a}(a>0),B={x|x2-5x+4≤0}.
(1)若“x∈A”是“x∈B”的必要不充分條件,求實數a的取值范圍;
(2)對任意x∈B,不等式x2-mx+4≥0都成立,求實數m的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com