
| A. | -14 | B. | -9 | C. | 9 | D. | 14 |
分析 可分別以直線AC,AB為x,y軸,建立平面直角坐標系,根據條件便可求出點A,B,C,D的坐標,進而求出點E的坐標,從而得出向量$\overrightarrow{AE},\overrightarrow{EB}$的坐標,這樣進行數量積的坐標運算即可求出$\overrightarrow{AE}•\overrightarrow{EB}$的值.
解答 解:如圖,分別以邊AC,AB所在直線為x,y軸,建立平面直角坐標系,則: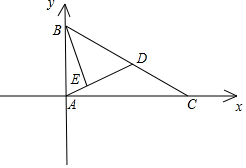
$A(0,0),B(0,6\sqrt{3}),C(6,0),D(3,3\sqrt{3})$;
$\overrightarrow{AE}=\frac{1}{2}\overrightarrow{ED}$;
∴$\overrightarrow{AE}=\frac{1}{3}\overrightarrow{AD}$=$\frac{1}{3}(3,3\sqrt{3})$;
∴$\overrightarrow{AE}$=$(1,\sqrt{3})$,$E(1,\sqrt{3})$,$\overrightarrow{EB}=(-1,5\sqrt{3})$;
∴$\overrightarrow{AE}•\overrightarrow{EB}=-1+15=14$.
故選:D.
點評 考查建立平面直角坐標系,通過坐標解決向量問題的方法,能求平面上點的坐標,以及向量數乘的幾何意義,數量積的坐標運算.


科目:高中數學 來源: 題型:選擇題
| A. | 16π | B. | 25π | C. | 36π | D. | 64π |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{π}{3}$ | B. | $\frac{π}{2}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
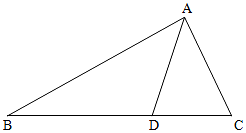 如圖,在△ABC中,點D在BC邊上,∠CAD=$\frac{π}{4}$,AC=$\frac{7}{2}$,cos∠ADB=-$\frac{\sqrt{2}}{10}$.
如圖,在△ABC中,點D在BC邊上,∠CAD=$\frac{π}{4}$,AC=$\frac{7}{2}$,cos∠ADB=-$\frac{\sqrt{2}}{10}$.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com