【題目】已知函數
，
.
（1）討論
的單調性；
（2）若有兩個極值點
，
，且
，證明：
.
【答案】(1) 見解析.
(2)證明見解析.
【解析】分析：(1)先求導數，再根據二次方程
=0根得情況分類討論：當
時，
.∴
在
上單調遞減. 當
時，根據兩根大小再分類討論對應單調區間， (2)先化簡不等式
消m得
，再利用導數研究
，
單調性，得其最小值大于-1，即證得結果.
詳解：（1）由
，得
，
.
設
，.
當時，即
時，
，.
∴在上單調遞減.
當時，即
時，
令
，得
，
，
.
當
時，
，
在
上，
，在
上，
，
∴在
上單調遞增，在
上單調遞減.
綜上，當時，在上單調遞減，
當時，在
，
上單調遞減，在
上單調遞增，
當
時，在
上單調遞增，在上單調遞減.
（2）∵有兩個極值點
，
，且，
∴由（1）知有兩個不同的零點，，
，，且，此時，
，
要證明
，只要證明
.
∵
，∴只要證明成立.
∵
，∴
.
設，，
則
，
當時，
，
∴
在上單調遞增，
∴
，即，
∴有兩個極值點，，且
時，
.
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】定義在
上的函數
滿足
.當
時，
，當
時，
,則f（1）+f（2）+…+f（2015）=（ ）
A. 333 B. 336 C. 1678 D. 2015
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列說法正確的是（）
A. 銳角是第一象限的角，所以第一象限的角都是銳角;
B. 如果向量
，則
；
C. 在
中，記
，
，則向量
與
可以作為平面ABC內的一組基底；
D. 若
，
都是單位向量，則
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列
的前
項和為
，且
，
.
（1）求數列的通項公式；
（2）已知
，記
（
且
），是否存在這樣的常數
，使得數列
是常數列，若存在，求出的值；若不存在，請說明理由；
（3）若數列
，對于任意的正整數，均有
成立，求證：數列是等差數列.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某公司為了變廢為寶，節約資源，新上了一個從生活垃圾中提煉生物柴油的項目．經測算該項目月處理成本
（元）與月處理量
（噸）之間的函數關系可以近似地表示為：
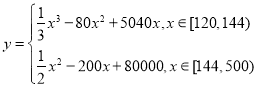，且每處理一噸生活垃圾，可得到能利用的生物柴油價值為
元，若該項目不獲利，政府將給予補貼．
（1）當
時，判斷該項目能否獲利？如果獲利，求出最大利潤；如果不獲利，則政府每月至少需要補貼多少元才能使該項目不虧損？
（2）該項目每月處理量為多少噸時，才能使每噸的平均處理成本最低？
查看答案和解析>>
科目：高中數學 來源： 題型：
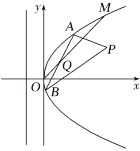
【題目】如圖所示，在直角坐標系
中，點
到拋物線
的準線的距離為
.點
是
上的定點，
，
是上的兩動點，且線段
的中點
在直線
上.
（Ⅰ）求曲線的方程及
的值；
（Ⅱ）記
，求
的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設
為正整數，集合
（
），對于集合
中的任意元素
和
，記
.
（1）當
時，若
，
，求
和
的值；
（2）當
時，設
是的子集，且滿足：對于中的任意元素
、
，當、相同時，是奇數，當、不同時，是偶數，求集合中元素個數的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
