
【題目】某化工廠從今年一月起,若不改善生產環境,按生產現狀,每月收入為80萬元,同時將受到環保部門的處罰,第一個月罰4萬元,以后每月增加2萬元.如果從今年一月起投資500萬元添加回收凈化設備(改造設備時間不計),一方面可以改善環境,另一方面可以大大降低原料成本,據測算,添加回收凈化設備并投產后的前4個月中的累計生產凈收入g(n)是生產時間![]() 個月的二次函數
個月的二次函數![]() 是常數
是常數![]() ,且前3個月的累計生產凈收入可達309萬元,從第5個月開始,每個月的生產凈收入都與第4個月相同,同時,該廠不但不受處罰,而且還將得到環保部門的一次性獎勵120萬元.
,且前3個月的累計生產凈收入可達309萬元,從第5個月開始,每個月的生產凈收入都與第4個月相同,同時,該廠不但不受處罰,而且還將得到環保部門的一次性獎勵120萬元.
(1)求前6個月的累計生產凈收入g(6)的值;
(2)問經過多少個月,投資開始見效,即投資改造后的純收入多于不改造的純收入.
 天天練口算系列答案
天天練口算系列答案科目:高中數學 來源: 題型:
【題目】下列說法正確的是( )
①從勻速傳遞的產品生產流水線上,質檢員每10分鐘從中抽取一件產品進行某項指標檢測,這樣的抽樣是分層抽樣.
②某地氣象局預報:5月9日本地降水概率為![]() ,結果這天沒下雨,這表明天氣預報并不科學.
,結果這天沒下雨,這表明天氣預報并不科學.
③在回歸分析模型中,殘差平方和越小,說明模型的擬合效果越好.
④在回歸直線方程![]() 中,當解釋變量
中,當解釋變量![]() 每增加1個單位時,預報變量
每增加1個單位時,預報變量![]() 增加0.1個單位.
增加0.1個單位.
A.①②B.③④C.①③D.②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 是橢圓
是橢圓![]() 的兩個焦點,
的兩個焦點,![]() 為坐標原點,離心率為
為坐標原點,離心率為![]() ,點
,點![]() 在橢圓上.
在橢圓上.
(1)求橢圓的標準方程;
(2)![]() 為橢圓上三個動點,
為橢圓上三個動點,![]() 在第二象限,
在第二象限,![]() 關于原點對稱,且
關于原點對稱,且![]() ,判斷
,判斷![]() 是否存在最小值,若存在,求出該最小值,并求出此時點
是否存在最小值,若存在,求出該最小值,并求出此時點![]() 的坐標,若不存在,說明理由.
的坐標,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】關于數列![]() ,給出下列命題:①數列
,給出下列命題:①數列![]() 滿足
滿足![]() ,則數列
,則數列![]() 為公比為2的等比數列;②“
為公比為2的等比數列;②“![]() ,
,![]() 的等比中項為
的等比中項為![]() ”是“
”是“![]() ”的充分不必要條件:③數列
”的充分不必要條件:③數列![]() 是公比為
是公比為![]() 的等比數列,則其前
的等比數列,則其前![]() 項和
項和![]() ;④等比數列
;④等比數列![]() 的前
的前![]() 項和為
項和為![]() ,則
,則![]() ,
,![]() ,
,![]() 成等比數列,其中假命題的序號是( )
成等比數列,其中假命題的序號是( )
A.②B.②④C.①②④D.①③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() 是實數.
是實數.
(1)若函數![]() 是定義在
是定義在![]() 上的奇函數,求
上的奇函數,求![]() 的值,并求方程
的值,并求方程![]() 的解;
的解;
(2)若![]() 對任意的
對任意的![]() 恒成立,求
恒成立,求![]() 的取值范圍;
的取值范圍;
(3)若![]() ,方程
,方程![]() 有解,求實數
有解,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校為了選拔學生參加“XX市中學生知識競賽”,先在本校進行選拔測試,若該校有100名學生參加選拔測試,并根據選拔測試成績作出如圖所示的頻率分布直方圖.
(1)根據頻率分布直方圖,估算這100名學生參加選拔測試的平均成績;
(2)該校推薦選拔測試成績在110以上的學生代表學校參加市知識競賽,為了了解情況,在該校推薦參加市知識競賽的學生中隨機抽取2人,求選取的兩人的選拔成績在頻率分布直方圖中處于不同組的概率.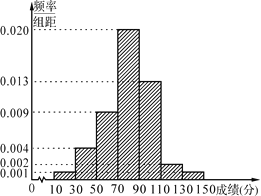
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com