【題目】已知函數f（x）=2sinxcosx+2 
cos2x﹣ ．
（1）求函數f（x）的單調減區間；
（2）在△ABC中，a，b，c分別是角A，B，C的對邊，已知a=1，b= 
，f（A﹣ 
）= ，求角C．
【答案】
（1）解：f（x）=2sinxcosx+2 
cos2x﹣ =sin2x+ cos2x=2sin（2x+ 
）．
由2kπ+ 
≤2x+ ≤2kπ+ 
，得x∈[kπ+ 
，kπ+ 
]（k∈Z），
因此f（x）的單調遞減區間為[kπ+ ，kπ+ ]（k∈Z）
（2）解：由f（A﹣ 
）=2sin[2（A﹣ ）+ ]=2sin2A= ，
又a＜b，所以A為銳角，則A= ．
由正弦定理得 
sinB= 
= 
，
當B= 
時，C=π﹣ ﹣ = ；
當B= 
時，C=π﹣ ﹣ =
【解析】（1）根據二倍角公式及輔助角公式將f（x）化簡，求得f（x）=2sin（2x+ ），根據正弦函數的單調性求得函數f（x）的單調減區間；（2）f（A﹣ ）= ，代入（1）求得sin2A= 
，由三角形的性質a＜b，求得A，利用正弦定理求得sinB，分類討論B的取值，分別求得角C．
【考點精析】掌握正弦定理的定義是解答本題的根本，需要知道正弦定理:
．
新題型全程檢測期末沖刺100分系列答案科目：高中數學 來源： 題型：
【題目】設f（x）是連續的偶函數，且當x＞0時，f（x）是單調函數，則滿足f（x）=f（ 
）的所有x之和為（ ）
A.﹣4031
B.﹣4032
C.﹣4033
D.﹣4034
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知△ABC中，A(1，－4)，B(6，6)，C(－2，0)．求：
（1）△ABC中平行于BC邊的中位線所在直線的一般式方程和截距式方程；
（2）BC邊的中線所在直線的一般式方程，并化為截距式方程．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）= 
在點（1，f（1））處的切線與x軸平行．
（1）求實數a的值及f（x）的極值；
（2）若對任意x1 ， x2∈[e2 ， +∞），有| 
|＞ 
，求實數k的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設點P（x，y）是曲線a|x|+b|y|=1（a≥0，b≥0）上任意一點，其坐標（x，y）均滿足 
，則 
a+b取值范圍為（ ）
A.（0，2]
B.[1，2]
C.[1，+∞）
D.[2，+∞）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】正四棱錐P﹣ABCD，B1為PB的中點，D1為PD的中點，則兩個棱錐A﹣B1CD1 ， P﹣ABCD的體積之比是（ ）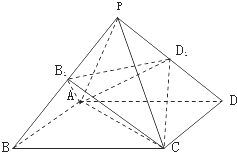 
A.1：4
B.3：8
C.1：2
D.2：3
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
