
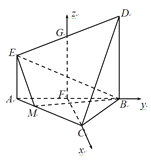
【題目】如圖,已知等邊![]() 與直角梯形
與直角梯形![]() 所在的平面互相垂直,且
所在的平面互相垂直,且![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)證明:直線![]() 平面
平面![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)證明見解析;(2)![]()
【解析】
(1)連接![]() 交于
交于![]() 點
點![]() ,連接
,連接![]() ,則
,則![]() ,
,![]() 得
得![]() ,則
,則![]() ,則
,則![]() 平面
平面![]() ;
;
(2)解:取![]() 中點
中點![]() ,
,![]() 中點
中點![]() ,連接
,連接![]() ,
,![]() ,則
,則![]() ,可證
,可證![]() 平面
平面![]() ,則
,則![]() 平面
平面![]() ,分別以
,分別以![]() ,
,![]() ,
,![]() 所在直線為
所在直線為![]() 軸,
軸,![]() 軸,
軸,![]() 軸建立空間直角坐標系,利用平面的法向量與直線的方向向量的夾角的余弦值即可求出答案.
軸建立空間直角坐標系,利用平面的法向量與直線的方向向量的夾角的余弦值即可求出答案.
(1)證明:連接![]() 交于
交于![]() 點
點![]() ,連接
,連接![]() ,
,

∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,∴
,∴![]() ,
,
又∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ;
;
(2)解:取![]() 中點
中點![]() ,
,![]() 中點
中點![]() ,連接
,連接![]() ,
,![]() ,
,
∴![]() ,
,
又∵![]() 等邊,∴
等邊,∴![]() ;
;
∵平面![]() 平面
平面![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
分別以![]() ,
,![]() ,
,![]() 所在直線為
所在直線為![]() 軸,
軸,![]() 軸,
軸,![]() 軸建立如圖所示的空間直角坐標系,
軸建立如圖所示的空間直角坐標系,
則![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴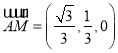 ,
,![]() ,
,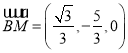 ,
,![]() ,
,![]() ,
,
設平面![]() 的一個法向量為
的一個法向量為![]() ,
,
則由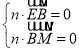 得一個
得一個![]() ,
,
設直線![]() 與平面
與平面![]() 所成角為
所成角為![]() ,
,
則![]() ,
,
∴直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,曲線C的參數方程為![]() (θ為參數),在以O為極點,x軸的正半軸為極軸的極坐標系中,直線l:
(θ為參數),在以O為極點,x軸的正半軸為極軸的極坐標系中,直線l: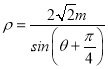 (m為常數).
(m為常數).
(1)求曲線C的普通方程與直線l的直角坐標方程;
(2)若直線l與曲線C相交于A、B兩點,當|AB|=4時,求實數m的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】實現國家富強.民族復興.人民幸福是“中國夢”的本質內涵.某商家計劃以“全民健身促健康,同心共筑中國夢”為主題舉辦一次有獎消費活動,此商家先把某品牌乒乓球重新包裝,包裝時在每個乒乓球上印上“中”“國”“夢”三個字樣中的一個,之后隨機裝盒(1盒4個球),并規定:若顧客購買的一盒球印的是同一個字,則此顧客獲得一等獎;若顧客購買的一盒球集齊了“中”“國”二字且僅有此二字,則此顧客獲得二等獎;若顧客購買的一盒球集齊了“中”“國”“夢”三個字,則此顧客獲得三等獎,其它情況不設獎,則顧客購買一盒乒乓球獲獎的概率是_____________.
查看答案和解析>>
科目:高中數學 來源: 題型:
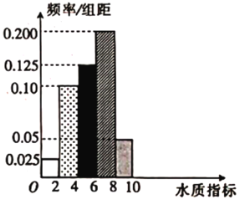
【題目】新《水污染防治法》已由中華人民共和國第十二屆全國人民代表大會常務委員會第二十八次會議于2017年6月27日通過,自2018年1月1日起施行.2018年3月1日,某縣某質檢部門隨機抽取了縣域內100眼水井,檢測其水質總體指標.
羅斯水質指數 | 02 | 24 | 46 | 68 | 810 |
水質狀況 | 腐敗污水 | 嚴重污染 | 污染 | 輕度污染 | 純凈 |
(1)求所抽取的100眼水井水質總體指標值的樣本平均數![]() (同一組中的數據用該組區間的中點值作代表).
(同一組中的數據用該組區間的中點值作代表).
(2)①由直方圖可以認為,100眼水井水質總體指標值![]() 服從正態分布
服從正態分布![]() ,利用該正態分布,求
,利用該正態分布,求![]() 落在(5.21,5.99)內的概率;
落在(5.21,5.99)內的概率;
②將頻率視為概率,若某鄉鎮抽查5眼水井的水質,記這5眼水井水質總體指標值位于(6,10)內的井數為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
附:①計算得所抽查的這100眼水井總體指標的標準差為![]() ;
;
②若![]() ,則
,則![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某家政公司對部分員工的服務進行民意調查,調查按各項服務標準進行量化評分,嬰幼兒保姆部對40~50歲和20~30歲各20名女保姆的調查結果如下:
分數 年齡 |
|
|
|
|
|
40~50歲 | 0 | 2 | 4 | 7 | 7 |
20~30歲 | 3 | 5 | 5 | 5 | 2 |
(1)若規定評分不低于80分為優秀保姆,試分別估計這兩個年齡段保姆的優秀率;
(2)按照大于或等于80分為優秀保姆,80分以下為非優秀保姆統計.作出![]() 列聯表,并判斷能否有
列聯表,并判斷能否有![]() 的把握認為對保姆工作質量的評價是否優秀與年齡有關.
的把握認為對保姆工作質量的評價是否優秀與年齡有關.
(3)從所有成績在70分以上的人中按年齡利用分層抽樣抽取10名保姆,再從這10人中選取3人給大家作經驗報告,設抽到40~50歲的保姆的人數為![]() ,求出
,求出![]() 的分布列與期望值.
的分布列與期望值.
下面的臨界值表供參考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
參考公式: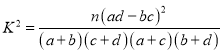 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() ,直線
,直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點,
兩點,![]() 為坐標原點.
為坐標原點.
(1)若直線![]() 過橢圓
過橢圓![]() 的右焦點
的右焦點![]() ,求
,求![]() 的面積;
的面積;
(2)若![]() ,試問橢圓
,試問橢圓![]() 上是否存在點
上是否存在點![]() ,使得四邊形
,使得四邊形![]() 為平行四邊形?若存在,求出
為平行四邊形?若存在,求出![]() 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}為正項等比數列,a1=1,數列{bn}滿足b2=3,a1b1+a2b2+a3b3+…+anbn=3+(2n﹣3)2n.
(1)求an;
(2)求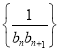 的前n項和Tn.
的前n項和Tn.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的離心率為
的離心率為![]() ,左右頂點分別為
,左右頂點分別為![]() ,
,![]() ,右焦點為
,右焦點為![]() ,
,![]() 為橢圓上異于
為橢圓上異于![]() ,
,![]() 的動點,且
的動點,且![]() 面積的最大值為
面積的最大值為![]() .
.
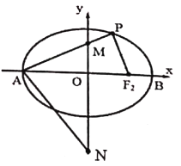
(1)求橢圓![]() 的方程;
的方程;
(2)設直線![]() 與
與![]() 軸交于
軸交于![]() 點,過點
點,過點![]() 作
作![]() 的平行線交
的平行線交![]() 軸與點
軸與點![]() ,試探究是否存在定點
,試探究是否存在定點![]() ,使得以
,使得以![]() 為直徑的圓恒過定點
為直徑的圓恒過定點![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com