
已知函數f(x)=4x3-3x2cosθ+ ,其中x∈R,θ為參數,且0≤θ≤2π.
,其中x∈R,θ為參數,且0≤θ≤2π.
(1)當 時,判斷函數f(x)是否有極值;
時,判斷函數f(x)是否有極值;
(2)要使函數f(x)的極小值大于零,求參數θ的取值范圍;
(3)若對(2)中所求的取值范圍內的任意參數θ,函數f(x)在區間(2A-1,A)內都是增函數,求實數A的取值范圍.
(1) 無極值;(2) θ的取值范圍為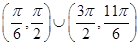 ;(3) A的取值范圍是
;(3) A的取值范圍是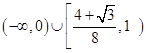 .
.
解析試題分析:(1)由題得f(x)=4x3 ,由冪函數性質知,在R上為增函數,無極值;(2)對原函數求導且令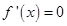 ,解得
,解得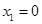 或
或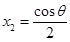 ,當
,當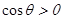 時,可求得極小值
時,可求得極小值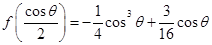 ,令
,令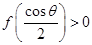 得
得 ,當
,當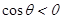 ,所求極小值不會小于零,可得
,所求極小值不會小于零,可得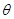 范圍;(3) 函數f(x)在區間(2A-1,A)內都是增函數,則A需滿足不等式組
范圍;(3) 函數f(x)在區間(2A-1,A)內都是增函數,則A需滿足不等式組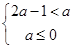 或
或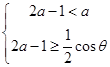 ,解得
,解得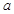 的范圍.
的范圍.
解:(1)當 時,f(x)=4x3,則f(x)在(-∞,+∞)內是增函數,故無極值. 2分
時,f(x)=4x3,則f(x)在(-∞,+∞)內是增函數,故無極值. 2分
(2)f′(x)=12x2-6xcosθ,
令f′(x)=0,得x1=0,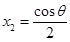 . 3分
. 3分
當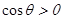 時,容易判斷f(x)在(-∞,0],
時,容易判斷f(x)在(-∞,0], 上是增函數,在
上是增函數,在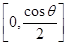 上是減函數,
上是減函數,
故f(x)在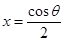 處取得極小值
處取得極小值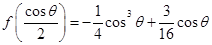 5分
5分
由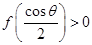 ,即
,即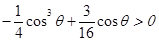 ,可得
,可得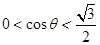 .
.
由于0≤θ≤2π,故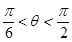 或
或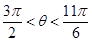 . 7分
. 7分
同理,可知當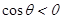 時,f(x)在x=0處取得極小值
時,f(x)在x=0處取得極小值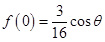 ,此時,當f(0)>0時,
,此時,當f(0)>0時,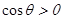 ,與
,與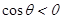 相矛盾,所以當
相矛盾,所以當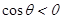 時,f(x)的極小值不會大于零.
時,f(x)的極小值不會大于零.
綜上,要使函數f(x)在(-∞,+∞)的極小值大于零,θ的取值范圍為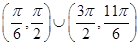 . 9分
. 9分
(3)由(2),知函數f(x)在區間(-∞,0]與 內都是增函數,由題設:函數在(2A-1,A)內是增函數,則A需滿足不等式組
內都是增函數,由題設:函數在(2A-1,A)內是增函數,則A需滿足不等式組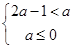 或
或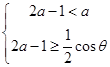 (其中θ∈
(其中θ∈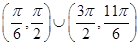 時,
時,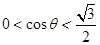 ). 12分
). 12分
從而可以解得A≤0或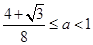 ,
,
即A的取值范圍是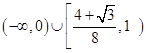 . 14分
. 14分
考點:函數的極值,由三角函數求角的范圍,函數的單調性.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:解答題
如圖,某污水處理廠要在一正方形污水處理池 內修建一個三角形隔離區以投放凈化物質,其形狀為三角形
內修建一個三角形隔離區以投放凈化物質,其形狀為三角形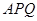 ,其中
,其中 位于邊
位于邊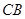 上,
上,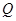 位于邊
位于邊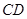 上.已知
上.已知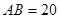 米,
米,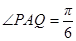 ,設
,設 ,記
,記 ,當
,當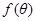 越大,則污水凈化效果越好.
越大,則污水凈化效果越好.
(1)求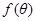 關于的函數解析式,并求定義域;
關于的函數解析式,并求定義域;
(2)求 最大值,并指出等號成立條件?
最大值,并指出等號成立條件?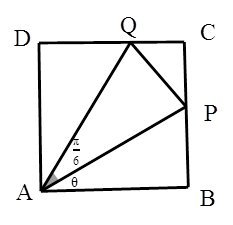
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(2014·濟南模擬)已知函數f(x)=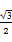 sinωx-sin2
sinωx-sin2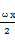 +
+ (ω>0)的最小正周期為π.
(ω>0)的最小正周期為π.
(1)求ω的值及函數f(x)的單調遞增區間.
(2)當x∈ 時,求函數f(x)的取值范圍.
時,求函數f(x)的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數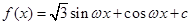 (
( ,
,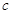 是實數常數)的圖像上的一個最高點
是實數常數)的圖像上的一個最高點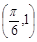 ,與該最高點最近的一個最低點是
,與該最高點最近的一個最低點是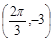 ,
,
(1)求函數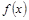 的解析式及其單調增區間;
的解析式及其單調增區間;
(2)在銳角三角形△ABC中,角A、B、C所對的邊分別為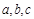 ,且
,且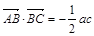 ,角A的取值范圍是區間M,當
,角A的取值范圍是區間M,當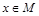 時,試求函數
時,試求函數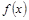 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com