
分析 (Ⅰ)當a=b=c=1時,$f(x)=1+{(\frac{1}{2})^x}+{(\frac{1}{4})^x}$,則f(x)在(-∞,0)上單調遞減,進而可得f(x)在(-∞,0)上的值域為(3,+∞),并可判斷出函數f(x)在(-∞,0)上沒有上界.
(Ⅱ) 由題意知,|f(x)|≤3在[0,+∞)上恒成立.令$t={(\frac{1}{2})^x},0<t≤1$,可得實數a的取值范圍.
(Ⅲ)已知s為正整數,當a=1,b=-1,c=0時,存在λ=10使得對任意的n∈N•,不等式s≤λf(n)≤s+2恒成立,分類討論,可得結論.
解答 解:(Ⅰ)當a=b=c=1時,$f(x)=1+{(\frac{1}{2})^x}+{(\frac{1}{4})^x}$,
易知f(x)在(-∞,0)上單調遞減,∴f(x)>f(0)=3.
∴f(x)在(-∞,0)上的值域為(3,+∞).
∴不存在常數M>0,使得|f(x)|≤M成立,
∴f(x)在(-∞,0)上沒有上界.
(Ⅱ) 由題意知,|f(x)|≤3在[0,+∞)上恒成立.
令$t={(\frac{1}{2})^x},0<t≤1$,
∴題意等價于-3≤1+at+t2≤3在t∈(0,1]上恒成立.
$?-\frac{4}{t}-t≤a≤\frac{2}{t}-t$在t∈(0,1]上恒成立.$?{({-\frac{4}{t}-t})_{max}}≤a≤{({\frac{2}{t}-t})_{min}}$.
設$g(t)=-\frac{4}{t}-t,h(t)=\frac{2}{t}-t,0<t≤1$易知h(t)在(0,1]上遞減.
令0<t1<t2≤1,有$g({t_1})-g({t_2})=(-\frac{4}{t_1}-{t_1})-(-\frac{4}{t_2}-{t_2})=\frac{{({t_2}-{t_1})({t_2}{t_1}-4)}}{{{t_1}{t_2}}}<0$
∴g(t)在(0,1]上遞增.
∴g(t)max=g(1)=-5,h(t)min=h(1)=1.
∴實數a的取值范圍是[-5,1].
(Ⅲ)當a=1,b=-1,c=0時,$f(n)=1+{(-\frac{1}{2})^n}>0$,
∴題意等價于$\frac{s}{{1+{{(-\frac{1}{2})}^n}}}≤λ≤\frac{s+2}{{1+{{(-\frac{1}{2})}^n}}}$對任意的n∈N•恒成立.
∵當n為正奇數時,$\frac{1}{2}≤1+{(-\frac{1}{2})^n}<1$;當n為正偶數時,$1<1+{(-\frac{1}{2})^n}≤\frac{5}{4}$,
∴$2s≤λ≤\frac{4}{5}(s+2)$.
∴當$2s>\frac{4}{5}(s+2)$,即$s>\frac{4}{3}$時,不存在滿足題意的λ;
當$2s≤\frac{4}{5}(s+2)$,即$0<s≤\frac{4}{3}$時,存在滿足題意的λ,且$λ∈[{2s,\frac{4}{5}(s+2)}]$.
∵s為正整數,∴s=1.
此時,$λ∈[{2,\frac{12}{5}}]$,∵λ為整數,∴λ=10.
點評 本題考查的知識點是復合函數的單調性,二次函數的圖象和性質,函數恒成立問題,轉化思想,難度中檔.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中數學 來源: 題型:解答題
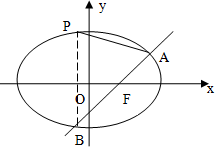 已知橢圓$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1,(a>b>0)$的離心率為$e=\frac{1}{2}$,直線x+2y-1=0經過橢圓的一個焦點;
已知橢圓$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1,(a>b>0)$的離心率為$e=\frac{1}{2}$,直線x+2y-1=0經過橢圓的一個焦點;查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 0 | B. | 1 | C. | 2 | D. | 1或2 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | f(a)<0,f(b)<0 | B. | f(a)>0,f(b)>0 | C. | f(a)>0,f(b)<0 | D. | f(a)<0,f(b)>0 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
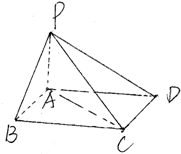 如圖四棱錐P-ABCD中,底面ABCD為平行四邊形,∠ABC=60°,PA=AB=1,BC=2,PA⊥底面ABCD
如圖四棱錐P-ABCD中,底面ABCD為平行四邊形,∠ABC=60°,PA=AB=1,BC=2,PA⊥底面ABCD查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com