
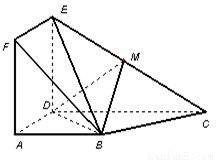
如圖,正方形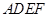 與梯形
與梯形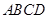 所在的平面互相垂直,
所在的平面互相垂直,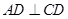 ,
,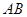 ∥
∥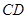 ,
,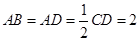 ,點
,點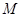 在線段
在線段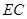 上.
上.
(I)當點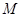 為
為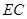 中點時,求證:
中點時,求證: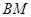 ∥平面
∥平面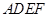 ;
;
(II)當平面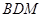 與平面
與平面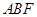 所成銳二面角的余弦值為
所成銳二面角的余弦值為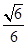 時,求三棱錐
時,求三棱錐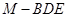 的體積.
的體積.
(I)建立空間直角坐標系,證明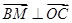 ,進而得證;(II)
,進而得證;(II)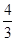
【解析】
試題分析:
(I )以直線DA,BC,DE分別為x軸,y軸,z軸建立空間直角坐標系,
則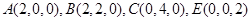 ,所以
,所以 ,
,
所以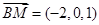 ,
2分
,
2分
又 是平面
是平面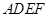 的一個法向量,
的一個法向量, ,所以
,所以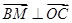 ,
,
所以 ∥平面
∥平面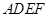 .
4分
.
4分
(II)設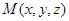 ,則
,則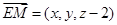 ,又
,又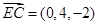 ,
,
則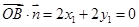 ,
,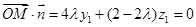 ,
,
取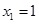 得
得
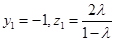 , 即
, 即 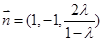 ,
,
又由題設,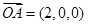 是平面
是平面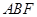 的一個法向量, 8分
的一個法向量, 8分
∴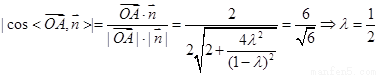 10分
10分
即點 為
為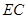 中點,此時,
中點,此時,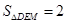 ,
,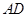 為三棱錐
為三棱錐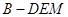 的高,
的高,
∴ 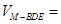
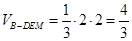 .
12分
.
12分
考點:本小題主要考查線面平行,二面角,三棱錐的體積計算.
點評:解決立體幾何問題,可以用相關的定理證明,也可以用空間向量證明,利用空間向量也要依據相應的判定定理和性質定理,并且要注意各個角的取值范圍.


 黃岡360度定制密卷系列答案
黃岡360度定制密卷系列答案 陽光考場單元測試卷系列答案
陽光考場單元測試卷系列答案 名校聯盟沖刺卷系列答案
名校聯盟沖刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:高中數學 來源: 題型:
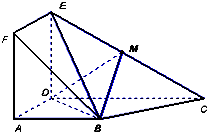 如圖,正方形ADEF與梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=
如圖,正方形ADEF與梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=| 1 |
| 2 |
| ||
| 6 |
查看答案和解析>>
科目:高中數學 來源: 題型:
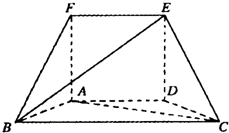 如圖,正方形ADEF所在平面和等腰梯形所在平面ABCD垂直,已知BC=2AD=4,∠ABC=60°,BF⊥AC.
如圖,正方形ADEF所在平面和等腰梯形所在平面ABCD垂直,已知BC=2AD=4,∠ABC=60°,BF⊥AC.查看答案和解析>>
科目:高中數學 來源:2011-2012學年海南省高三高考極限壓軸卷理科數學試卷(解析版) 題型:填空題
(本小題滿分12分)
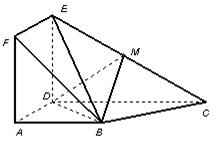
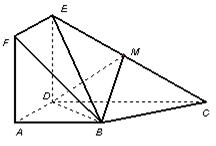
如圖,正方形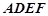 與梯形
與梯形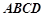 所在的平面互相垂直,
所在的平面互相垂直,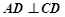 ,
,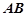 ∥
∥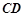 ,
,
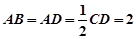 ,點
,點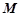 在線段
在線段 上.
上.
(I)當點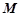 為
為 中點時,求證:
中點時,求證: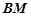 ∥平面
∥平面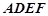 ;
;
(II)當平面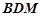 與平面
與平面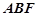 所成銳二面角的余弦值為
所成銳二面角的余弦值為 時,求三棱錐
時,求三棱錐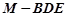 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
如圖,正方形![]() 與梯形
與梯形![]() 所在的平面互相垂直,
所在的平面互相垂直,![]() ,
,![]() ∥
∥![]() ,
,
![]() ,點
,點![]() 在線段
在線段![]() 上.
上.
(I)當點![]() 為
為![]() 中點時,求證:
中點時,求證:![]() ∥平面
∥平面![]() ;
;
(II)當平面![]() 與平面
與平面![]() 所成銳二面角的余弦值為
所成銳二面角的余弦值為![]() 時,求三棱錐
時,求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com