
【題目】已知函數(shù)![]() .
.
(1)討論![]() 的單調(diào)性;
的單調(diào)性;
(2)若![]() ,試判斷
,試判斷![]() 的零點個數(shù).
的零點個數(shù).
【答案】(1)當(dāng)![]() 時,
時,![]() 在
在![]() 上是增函數(shù),
上是增函數(shù),
當(dāng)![]() ,
,![]() 在
在![]() 上是增函數(shù),在
上是增函數(shù),在![]() 上是減函數(shù),在
上是減函數(shù),在![]() 上是增函數(shù),
上是增函數(shù),
當(dāng)![]() 時,
時,![]() 在
在![]() 上是增函數(shù),在
上是增函數(shù),在![]() 上是減函數(shù),在
上是減函數(shù),在![]() 上是增函數(shù);
上是增函數(shù);
(2)1
【解析】
(1)對![]() 求導(dǎo)后對
求導(dǎo)后對![]() 進行分類討論,找到
進行分類討論,找到![]() 和
和![]() 的區(qū)間,即為
的區(qū)間,即為![]() 的單調(diào)區(qū)間.
的單調(diào)區(qū)間.
(2)由(1)可知![]() 時,
時,![]() 有極大值
有極大值![]() 和極小值
和極小值![]() ,研究他們的正負,并且找到令
,研究他們的正負,并且找到令![]() 的點,根據(jù)零點存在定理,找出零點個數(shù).
的點,根據(jù)零點存在定理,找出零點個數(shù).
(1)函數(shù)![]() 的定義域為
的定義域為![]() ,
,![]() ,令
,令![]() ,則
,則![]() ,
,![]() ,
,
(i)若![]() ,則
,則![]() 恒成立,所以
恒成立,所以![]() 在
在![]() 上是增函數(shù),
上是增函數(shù),
(ii)若![]() ,則
,則![]() ,
,
當(dāng)![]() 時,
時,![]() ,
,![]() 是增函數(shù),
是增函數(shù),
當(dāng)![]() 時,
時,![]() ,
,![]() 是減函數(shù),
是減函數(shù),
當(dāng)![]() 時,
時,![]() ,
,![]() 是增函數(shù),
是增函數(shù),
(iii)若![]() ,則
,則![]() ,
,
當(dāng)![]() 時,
時,![]() ,
,![]() 是增函數(shù),
是增函數(shù),
當(dāng)![]() 時,
時,![]() ,
,![]() 是減函數(shù),
是減函數(shù),
當(dāng)![]() 時,
時,![]() ,
,![]() 是增函數(shù),
是增函數(shù),
綜上所述:當(dāng)![]() 時,
時,![]() 在
在![]() 上是增函數(shù),
上是增函數(shù),
當(dāng)![]() ,
,![]() 在
在![]() 上是增函數(shù),在
上是增函數(shù),在![]() 上是減函數(shù),在
上是減函數(shù),在![]() 上是增函數(shù),
上是增函數(shù),
當(dāng)![]() 時,
時,![]() 在
在![]() 上是增函數(shù),在
上是增函數(shù),在![]() 上是減函數(shù),在
上是減函數(shù),在![]() 上是增函數(shù);
上是增函數(shù);
(2)當(dāng)![]() 時,
時,
![]() 在
在![]() 上是增函數(shù),在
上是增函數(shù),在![]() 上是減函數(shù),在
上是減函數(shù),在![]() 上是增函數(shù),
上是增函數(shù),
所以![]() 的極小值為
的極小值為![]() ,
,
![]() 的極大值為
的極大值為![]() ,
,
設(shè)![]() ,其中
,其中![]() ,
,
![]() ,
,
所以![]() 在
在![]() 上是增函數(shù),
上是增函數(shù),
所以![]() ,
,
因為![]() ,
,
所以有且僅有1個![]() ,使
,使![]() .
.
所以當(dāng)![]() 時,
時,![]() 有且僅有1個零點.
有且僅有1個零點.


科目:高中數(shù)學(xué) 來源: 題型:
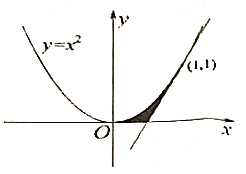
【題目】我國南北朝時期的數(shù)學(xué)家祖暅提出了計算體積的祖暅原理:“冪勢既同,則積不容異。”意思是:兩個等高的幾何體若在所有等高處的水平截面的面積相等,則這兩個幾何體的體積相等.已知曲線![]() ,直線
,直線![]() 為曲線
為曲線![]() 在點
在點![]() 處的切線.如圖所示,陰影部分為曲線
處的切線.如圖所示,陰影部分為曲線![]() 、直線
、直線![]() 以及
以及![]() 軸所圍成的平面圖形,記該平面圖形繞
軸所圍成的平面圖形,記該平面圖形繞![]() 軸旋轉(zhuǎn)一周所得的幾何體為
軸旋轉(zhuǎn)一周所得的幾何體為![]() .給出以下四個幾何體:
.給出以下四個幾何體:





① ② ③ ④
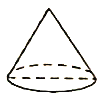
圖①是底面直徑和高均為![]() 的圓錐;
的圓錐;
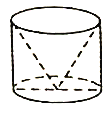
圖②是將底面直徑和高均為![]() 的圓柱挖掉一個與圓柱同底等高的倒置圓錐得到的幾何體;
的圓柱挖掉一個與圓柱同底等高的倒置圓錐得到的幾何體;
圖③是底面邊長和高均為![]() 的正四棱錐;
的正四棱錐;
圖④是將上底面直徑為![]() ,下底面直徑為
,下底面直徑為![]() ,高為
,高為![]() 的圓臺挖掉一個底面直徑為
的圓臺挖掉一個底面直徑為![]() ,高為
,高為![]() 的倒置圓錐得到的幾何體.
的倒置圓錐得到的幾何體.
根據(jù)祖暅原理,以上四個幾何體中與![]() 的體積相等的是( )
的體積相等的是( )
A. ①B. ②C. ③D. ④
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某中學(xué)的高二(1)班男同學(xué)![]() 名,女同學(xué)
名,女同學(xué)![]() 名,老師按照分層抽樣的方法組建了一個
名,老師按照分層抽樣的方法組建了一個![]() 人的課外興趣小組.
人的課外興趣小組.
(1)求某同學(xué)被抽到的概率及課外興趣小組中男、女同學(xué)的人數(shù);
(2)經(jīng)過一個月的學(xué)習(xí)、討論,這個興趣小組決定選出兩名同學(xué)做某項實驗,方法是先從小組里選出![]() 名同學(xué)做實驗,該同學(xué)做完后,再從小組內(nèi)剩下的同學(xué)中選
名同學(xué)做實驗,該同學(xué)做完后,再從小組內(nèi)剩下的同學(xué)中選![]() 名同學(xué)做實驗,求選出的兩名同學(xué)中恰有
名同學(xué)做實驗,求選出的兩名同學(xué)中恰有![]() 名女同學(xué)的概率;
名女同學(xué)的概率;
(3)實驗結(jié)束后,第一次做實驗的同學(xué)得到的實驗數(shù)據(jù)為![]() ,第二次做實驗的同學(xué)得到的實驗數(shù)據(jù)為
,第二次做實驗的同學(xué)得到的實驗數(shù)據(jù)為![]() ,請問哪位同學(xué)的實驗更穩(wěn)定?并說明理由.
,請問哪位同學(xué)的實驗更穩(wěn)定?并說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列命題正確的有________(填序號)
①已知![]() 或
或![]() ,
,![]() ,則p是q的充分不必要條件;
,則p是q的充分不必要條件;
②“函數(shù)![]() 的最小正周期為
的最小正周期為![]() ”是“
”是“![]() ”的必要不充分條件;
”的必要不充分條件;
③![]() 中,內(nèi)角A,B,C所對的邊分別為a,b,c,
中,內(nèi)角A,B,C所對的邊分別為a,b,c,![]() ,
,![]() ,則“
,則“![]() ”是“
”是“![]() 為等腰三角形”的必要不充分條件;
為等腰三角形”的必要不充分條件;
④若命題![]() “函數(shù)
“函數(shù)![]() 的值域為
的值域為![]() ”為真命題,則實數(shù)a的取值范圍是
”為真命題,則實數(shù)a的取值范圍是![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】我國南北朝時期的數(shù)學(xué)家祖暅提出了計算體積的祖暅原理:“冪勢既同,則積不容異。”意思是:兩個等高的幾何體若在所有等高處的水平截面的面積相等,則這兩個幾何體的體積相等.已知曲線![]() ,直線
,直線![]() 為曲線
為曲線![]() 在點
在點![]() 處的切線.如圖所示,陰影部分為曲線
處的切線.如圖所示,陰影部分為曲線![]() 、直線
、直線![]() 以及
以及![]() 軸所圍成的平面圖形,記該平面圖形繞
軸所圍成的平面圖形,記該平面圖形繞![]() 軸旋轉(zhuǎn)一周所得的幾何體為
軸旋轉(zhuǎn)一周所得的幾何體為![]() .給出以下四個幾何體:
.給出以下四個幾何體:


① ② ③ ④
圖①是底面直徑和高均為![]() 的圓錐;
的圓錐;
圖②是將底面直徑和高均為![]() 的圓柱挖掉一個與圓柱同底等高的倒置圓錐得到的幾何體;
的圓柱挖掉一個與圓柱同底等高的倒置圓錐得到的幾何體;
圖③是底面邊長和高均為![]() 的正四棱錐;
的正四棱錐;
圖④是將上底面直徑為![]() ,下底面直徑為
,下底面直徑為![]() ,高為
,高為![]() 的圓臺挖掉一個底面直徑為
的圓臺挖掉一個底面直徑為![]() ,高為
,高為![]() 的倒置圓錐得到的幾何體.
的倒置圓錐得到的幾何體.
根據(jù)祖暅原理,以上四個幾何體中與![]() 的體積相等的是( )
的體積相等的是( )
A. ①B. ②C. ③D. ④
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖所示的多面體是由一個直平行六面體被平面![]() 所截后得到的,其中
所截后得到的,其中![]() ,
,![]() ,
,![]() .
.
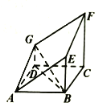
(1)求證:平面![]() 平面
平面![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知命題p:關(guān)于x的方程x![]() a在(1,+∞)上有實根;命題q:方程
a在(1,+∞)上有實根;命題q:方程![]() 1表示的曲線是焦點在x軸上的橢圓.
1表示的曲線是焦點在x軸上的橢圓.
(1)若p是真命題,求a的取值范圍;
(2)若p∧q是真命題,求a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() ,
,![]() 為橢圓上不與左右頂點重合的任意一點,
為橢圓上不與左右頂點重合的任意一點,![]() ,
,![]() 分別為
分別為![]() 的內(nèi)心、重心,當(dāng)
的內(nèi)心、重心,當(dāng)![]() 軸時,橢圓的離心率為( )
軸時,橢圓的離心率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com