
對于函數 ,若存在實數對(
,若存在實數對( ),使得等式
),使得等式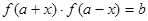 對定義域中的每一個
對定義域中的每一個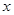 都成立,則稱函數
都成立,則稱函數 是“(
是“( )型函數”.
)型函數”.
(Ⅰ)判斷函數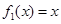 是否為 “(
是否為 “( )型函數”,并說明理由;
)型函數”,并說明理由;
(Ⅱ)若函數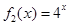 是“(
是“( )型函數”,求出滿足條件的一組實數對
)型函數”,求出滿足條件的一組實數對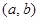 ;,
;,
(Ⅲ)已知函數 是“(
是“( )型函數”,對應的實數對
)型函數”,對應的實數對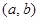 為
為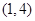 .當
.當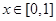 時,
時,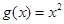
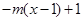
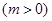 ,若當
,若當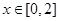 時,都有
時,都有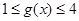 ,試求
,試求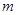 的取值范圍.
的取值范圍.
(Ⅰ)詳見解析;(Ⅱ)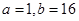 (答案還有其他可能);(Ⅲ)
(答案還有其他可能);(Ⅲ)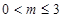
解析試題分析:(Ⅰ) 由給出的定義可知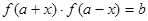 展開后的方程中如果不含x說明對任意x都成立,則函數
展開后的方程中如果不含x說明對任意x都成立,則函數 是“(
是“( )型函數” ,如果展開后的方程含x,則根據方程只能求出某個或某些x滿足要求而不是每一個x都符合,則函數
)型函數” ,如果展開后的方程含x,則根據方程只能求出某個或某些x滿足要求而不是每一個x都符合,則函數 不是“(
不是“( )型函數(Ⅱ)根據定義列出方程 ,滿足方程的實數對應有無數對,只取其中一對就可以(Ⅲ)難度系數較大,應先根據題意分析出當
)型函數(Ⅱ)根據定義列出方程 ,滿足方程的實數對應有無數對,只取其中一對就可以(Ⅲ)難度系數較大,應先根據題意分析出當 時,
時, 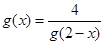 ,此時
,此時 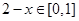 。根據已知
。根據已知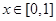 時,
時,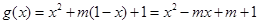 ,其對稱軸方程為
,其對稱軸方程為 。屬動軸定區間問題需分類討論,在每類中得出
。屬動軸定區間問題需分類討論,在每類中得出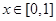 時
時 的值域即
的值域即 的值域,從而得出
的值域,從而得出 時
時 的值域,把兩個值域取并集即為
的值域,把兩個值域取并集即為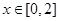 的
的 的值域,由
的值域,由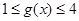 可知
可知 的值域是
的值域是 的子集,列出關于m的不等式即可求解。
的子集,列出關于m的不等式即可求解。
試題解析:(1)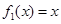 不是“(
不是“( )型函數”,因為不存在實數對
)型函數”,因為不存在實數對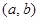 使得
使得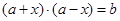 ,
,
即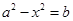 對定義域中的每一個
對定義域中的每一個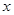 都成立;
都成立;
(2)由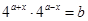 ,得
,得 ,所以存在實數對,
,所以存在實數對,
如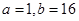 ,使得
,使得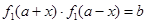 對任意的
對任意的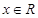 都成立;
都成立;
(3)由題意得, ,所以當
,所以當 時,
時, 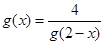 ,其中
,其中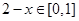 ,而
,而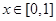 時,
時,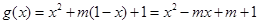 ,其對稱軸方程為
,其對稱軸方程為 .
.
當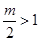 ,即
,即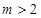 時,
時, 在
在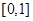 上的值域為
上的值域為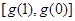 ,即
,即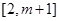 ,則
,則 在
在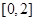 上的值域為
上的值域為 ,由題意得
,由題意得 ,從而
,從而 ;
;
當 ,即
,即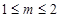 時,
時, 的值域為
的值域為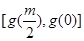 ,即
,即 ,則
,則 在
在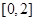 上的值域為
上的值域為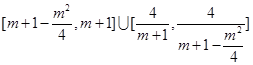 ,則由題意,得
,則由題意,得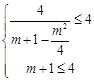 且
且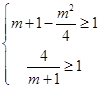 ,解得
,解得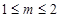 ;
;
當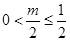 ,即
,即 時,
時, 的值域為
的值域為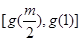 ,即
,即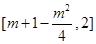 ,則
,則 在
在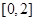 上的值域為
上的值域為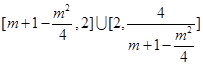 ,即
,即 ,則
,則 ,解得
,解得 .
.
綜上所述,所求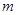 的取值范圍是
的取值范圍是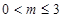


科目:高中數學 來源: 題型:解答題
 兩城相距
兩城相距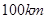 ,在兩地之間距
,在兩地之間距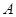 城
城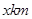 處
處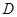 地建一核電站給
地建一核電站給 兩城供電.為保證城市安全,核電站距城市距離不得少于
兩城供電.為保證城市安全,核電站距城市距離不得少于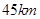 .已知供電費用(元)與供電距離(
.已知供電費用(元)與供電距離(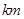 )的平方和供電量(億度)之積成正比,比例系數
)的平方和供電量(億度)之積成正比,比例系數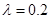 ,若
,若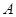 城供電量為
城供電量為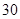 億度/月,
億度/月,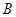 城為
城為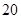 億度/月.
億度/月.
(Ⅰ)把月供電總費用 表示成
表示成 的函數,并求定義域;
的函數,并求定義域;
(Ⅱ)核電站建在距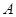 城多遠,才能使供電費用最小,最小費用是多少?
城多遠,才能使供電費用最小,最小費用是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某開發商用9000萬元在市區購買一塊土地建一幢寫字樓,規劃要求寫字樓每層建筑面積為2000平方米.已知該寫字樓第一層的建筑費用為每平方米4000元,從第二層開始,每一層的建筑費用比其下面一層每平方米增加100元.
(1)若該寫字樓共x層,總開發費用為y萬元,求函數y=f(x)的表達式;(總開發費用=總建筑費用+購地費用)
(2)要使整幢寫字樓每平方米的平均開發費用最低,該寫字樓應建為多少層?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖所示,一種醫用輸液瓶可以視為兩個圓柱的組合體.開始輸液時,滴管內勻速滴下球狀液體,其中球狀液體的半徑 毫米,滴管內液體忽略不計.
毫米,滴管內液體忽略不計.
(1)如果瓶內的藥液恰好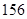 分鐘滴完,問每分鐘應滴下多少滴?
分鐘滴完,問每分鐘應滴下多少滴?
(2)在條件(1)下,設輸液開始后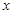 (單位:分鐘),瓶內液面與進氣管的距離為
(單位:分鐘),瓶內液面與進氣管的距離為 (單位:厘米),已知當
(單位:厘米),已知當 時,
時,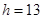 .試將
.試將 表示為
表示為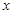 的函數.(注:
的函數.(注: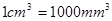 )
)
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數 ,點
,點 、
、 在函數
在函數 的圖象上,
的圖象上,
點 在函數
在函數 的圖象上,設
的圖象上,設
 .
.
(1)求數列 的通項公式;
的通項公式;
(2)記 ,求數列
,求數列 的前
的前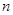 項和為
項和為 ;
;
(3)已知 ,記數列
,記數列 的前
的前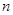 項和為
項和為 ,數列
,數列 的前
的前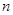 項和為
項和為 ,試比較
,試比較 與
與 的大小.
的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某工廠某種產品的年固定成本為250萬元,每生產 千件,需另投入成本為
千件,需另投入成本為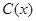 ,當年產量不足80千件時,
,當年產量不足80千件時, (萬元).當年產量不小于80千件時,
(萬元).當年產量不小于80千件時, (萬元).每件商品售價為0.05萬元.通過市場分析,該廠生產的商品能全部售完.
(萬元).每件商品售價為0.05萬元.通過市場分析,該廠生產的商品能全部售完.
(1)寫出年利潤 (萬元)關于年產量
(萬元)關于年產量 (千件)的函數解析式;
(千件)的函數解析式;
(2)年產量為多少千件時,該廠在這一商品的生產中所獲利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖所示, 是一個矩形花壇,其中AB= 4米,AD = 3米.現將矩形花壇
是一個矩形花壇,其中AB= 4米,AD = 3米.現將矩形花壇 擴建成一個更大的矩形花園
擴建成一個更大的矩形花園 ,要求:B在
,要求:B在 上,D在
上,D在 上,對角線
上,對角線 過C點, 且矩形
過C點, 且矩形 的面積小于64平方米.
的面積小于64平方米.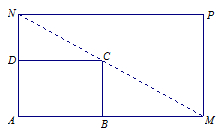
(Ⅰ)設 長為
長為 米,矩形
米,矩形 的面積為
的面積為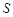 平方米,試用解析式將
平方米,試用解析式將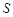 表示成
表示成 的函數,并寫出該函數的定義域;
的函數,并寫出該函數的定義域;
(Ⅱ)當 的長度是多少時,矩形
的長度是多少時,矩形 的面積最小?并求最小面積.
的面積最小?并求最小面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com