
【題目】如圖,在直二面角D﹣AB﹣E中,四邊形ABCD是邊長為2的正方形,AE=EB,點F在CE上,且BF⊥平面ACE; 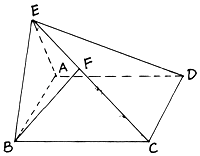
(1)求證:AE⊥平面BCE;
(2)求二面角B﹣AC﹣E的正弦值;
(3)求點D到平面ACE的距離.
【答案】
(1)證明:∵BF⊥平面ACE,∴BF⊥AE,
∵二面角D﹣AB﹣E為直二面角,
∴平面ABCD⊥平面ABE,
又BC⊥AB,∴BC⊥平面ABE,則BC⊥AE,
又BF平面BCE,BF∩BC=B,
∴AE⊥平面BCE
(2)法一、解:連接AC、BD交于G,連接FG,
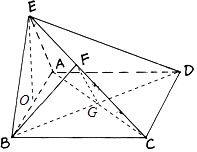
∵ABCD為正方形,∴BD⊥AC,
∵BF⊥平面ACE,BG⊥AC,∴AC⊥平面BFG,
∴FG⊥AC,即∠FGB為二面角B﹣AC﹣E的平面角,
由(1)可知,AE⊥平面BCE,∴AE⊥EB,
又AE=EB,AB=2,AE=BE= ![]() ,
,
在直角三角形BCE中,CE= ![]() =
= ![]() ,BF=
,BF= ![]() =
= ![]() ,
,
在正方形中,BG= ![]() ,在直角三角形BFG中,sin∠FGB=
,在直角三角形BFG中,sin∠FGB= ![]() ;
;
法二、以線段AB的中點為原點O,OE所在直線為x軸,AB所在直線為y軸,
過O點平行于AD的直線為z軸,建立空間直角坐標系O﹣xyz,如圖.
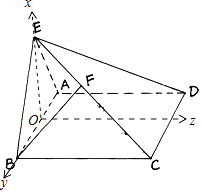
∵AE⊥面BCE,BE面BCE,∴AE⊥BE,
在Rt△AEB中,AB=2,O為AB的中點,
∴OE=1.∴A(0,﹣1,0),E(1,0,0),C(0,1,2),
![]() =(1,1,0),
=(1,1,0), ![]() =(0,2,2).
=(0,2,2).
設平面AEC的一個法向量為 ![]() =(x,y,z),
=(x,y,z),
則 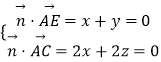 ,令x=1,得
,令x=1,得 ![]() =(1,﹣1,1)是平面AEC的一個法向量.
=(1,﹣1,1)是平面AEC的一個法向量.
又平面BAC的一個法向量為 ![]() =(1,0,0),
=(1,0,0),
∴cos< ![]() >=
>= ![]() =
= ![]() .
.
∴二面角B﹣AC﹣E的正弦值為 ![]()
(3)法一、由(2)可知,在正方形ABCD中,BG=DG,D到平面ACE的距離等于B到平面ACE的距離,
BF⊥平面ACE,線段BF的長度就是點B到平面ACE的距離,即為D到平面ACE的距離所以D到平面的距離為 ![]() .
.
法二、
解:∵AD∥z軸,AD=2,∴ ![]() =(0,0,2),
=(0,0,2),
∴點D到平面ACE的距離d=| ![]() ||cos<
||cos< ![]() >=
>= ![]() =
= ![]() .
.
【解析】(1)要證AE⊥平面BCE,只需證明AE垂直平面BCE內的兩條相交直線BF、BC即可;(2)連接AC、BD交于G,連接FG,說明∠FGB為二面角B﹣AC﹣E的平面角,然后求二面角B﹣AC﹣E的大小;(3)利用VD﹣ACE=VE﹣ACD , 求點D到平面ACE的距離,也可以利用空間直角坐標系,向量的數量積,證明垂直,求出向量的模.


 習題精選系列答案
習題精選系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x3﹣3x.
(1)求曲線y=f(x)在點x=2處的切線方程;
(2)若過點A(1,m)(m≠﹣2)可作曲線y=f(x)的三條切線,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=log2(ax2+4x+5).
(1)若f(1)<3,求a的取值范圍;
(2)若a=1,求函數f(x)的值域.
(3)若f(x)的值域為R,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=sin(2x+φ),其中φ為實數,若f(x)≤|f( ![]() )|對x∈R恒成立,且f(
)|對x∈R恒成立,且f( ![]() )>f(π),則f(x)的單調遞增區間是( )
)>f(π),則f(x)的單調遞增區間是( )
A.[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ](k∈Z)
](k∈Z)
B.[kπ,kπ+ ![]() ](k∈Z)
](k∈Z)
C.[kπ+ ![]() ,kπ+
,kπ+ ![]() ](k∈Z)
](k∈Z)
D.[kπ﹣ ![]() ,kπ](k∈Z)
,kπ](k∈Z)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數y=f(x)的導函數y=f′(x)的圖象如圖所示,則關于函數y=f(x),下列說法正確的是( ) 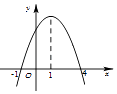
A.在x=﹣1處取得極大值
B.在區間[﹣1,4]上是增函數
C.在x=1處取得極大值
D.在區間[1,+∞)上是減函數
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x3+ax2+bx+c在x=﹣ ![]() 與x=1時都取得極值.
與x=1時都取得極值.
(1)求a、b的值與函數f(x)的單調區間;
(2)若對x∈[﹣1,2],不等式f(x)<c2恒成立,求c的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com