
【題目】已知函數![]() ,其中
,其中![]() .
.
![]() Ⅰ
Ⅰ![]() 如果曲線
如果曲線![]() 與x軸相切,求a的值;
與x軸相切,求a的值;
![]() Ⅱ
Ⅱ![]() 若
若![]() ,證明:
,證明:![]() ;
;
![]() Ⅲ
Ⅲ![]() 如果函數
如果函數![]() 在區間
在區間![]() 上不是單調函數,求a的取值范圍.
上不是單調函數,求a的取值范圍.
【答案】(Ⅰ)1(Ⅱ)詳見解析(Ⅲ)(![]() -ln2,1)
-ln2,1)
【解析】
(Ⅰ)先求導,再根據導數的幾何意義即可求出,
(Ⅱ)構造函數F(x)=f(x)-x=lnx-2x+ln2e,根據導數和函數單調性的關系以及最值得關系,即可證明
(Ⅲ)先求出函數g(x)在(1,e)上是單調函數a的范圍即可,求導,分離參數構造函數,求出函數的最值即可.
解:(I)求導.得f′(x)=![]() -1=
-1=![]()
∵曲線y=f(x)與x軸相切,∴此切線的斜率為0.
由f′(x)=0,解得x=1,
又由曲線y=(x)與x軸相切,得f(1)=-1+a=0
解得a=1.
(II)證明:由題意,f(x)=lnx-x+ln2e,
令函數F(x)=f(x)-x=lnx-2x+ln2e
求導,得F′(x)=![]() -2=
-2=![]()
由F′(x)=0,得x=![]() ,
,
當x變化時,F′(x)與F(x)的變化情況如下表所示:
x | (0, |
| ( |
F′(x) | + | 0 | - |
F(x) | 增 | 極大值 | 減 |
∴函數F(x)在(0,![]() )上單調遞增,在(
)上單調遞增,在(![]() ,+∞)單調遞減,
,+∞)單調遞減,
故當x=![]() 時,F(x)max=F(
時,F(x)max=F(![]() )=ln
)=ln![]() -1+ln2e=0,
-1+ln2e=0,
∴任給x∈(0,+∞),F(x)=f(x)-x≤0,即f(x)≤x,
(Ⅲ)由題意可得,g(x)=![]() ,
,
∴g′(x)=![]() ,
,
當g′(x)≥0時,在(1,e)上恒成立,函數g(x)單調遞增,
當g′(x)≤0時,在(1,e)上恒成立,函數g(x)單調遞減,
∴x-2lnx+1-2a≥0在(1,e)上恒成立,或x-2lnx+1-2a≤0在(1,e)上恒成立,
∴2a≤x-2lnx+1在(1,e)上恒成立,或2a≥x-2lnx+1在(1,e)上恒成立,
令h(x)=x-2lnx+1,
∴h′(x)=1-![]() =
=![]() ,
,
由h′(x)=0,解得x=2,
當x∈(1,2)時,h′(x)<0,函數h(x)單調遞減,
當x∈(2,e)時,h′(x)>0,函數h(x)單調遞增,
∵h(1)=2,h(e)=e-2+1=e-1,
∴h(x)max=h(1)=2
∴h(x)min=h(2)=3-2ln2,
∴2a≥2或2a≤3-2ln2,
∴a≥1或a<![]() -ln2,
-ln2,
∵函數![]() 在區間(1,e)上不是單調函數,
在區間(1,e)上不是單調函數,
∴![]() -ln2<a<1,
-ln2<a<1,
故a的取值范圍為(![]() -ln2,1).
-ln2,1).


 孟建平小學滾動測試系列答案
孟建平小學滾動測試系列答案科目:高中數學 來源: 題型:
【題目】小明口袋中有3張10元,3張20元(因紙幣有編號認定每張紙幣不同),現從中掏出紙幣超過45元的方法有_______種;若小明每次掏出紙幣的概率是等可能的,不放回地掏出4張,剛好是50元的概率為_______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 市某機構為了調查該市市民對我國申辦
市某機構為了調查該市市民對我國申辦![]() 年足球世界杯的態度,隨機選取了
年足球世界杯的態度,隨機選取了![]() 位市民進行調查,調查結果統計如下:
位市民進行調查,調查結果統計如下:
支持 | 不支持 | 合計 | |
男性市民 |
| ||
女性市民 |
| ||
合計 |
|
|
(1)根據已知數據,把表格數據填寫完整;
(2)利用(1)完成的表格數據回答下列問題:
(i)能否在犯錯誤的概率不超過![]() 的前提下認為支持申辦足球世界杯與性別有關;
的前提下認為支持申辦足球世界杯與性別有關;
(ii)已知在被調查的支持申辦足球世界杯的男性市民中有![]() 位退休老人,其中
位退休老人,其中![]() 位是教師,現從這
位是教師,現從這![]() 位退休老人中隨機抽取
位退休老人中隨機抽取![]() 人,求至多有
人,求至多有![]() 位老師的概率.
位老師的概率.
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在 △ABC 中,設 a,b,c 分別是角 A,B,C 的對邊,已知向量 ![]() = (a,sinC-sinB),
= (a,sinC-sinB),![]() = (b + c,sinA + sinB),且
= (b + c,sinA + sinB),且![]()
(1) 求角 C 的大小
(2) 若 c = 3, 求 △ABC 的周長的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某廠生產產品x件的總成本c(x)=1200+![]() x3(萬元),已知產品單價P(萬元)與產品件數x滿足:p2=
x3(萬元),已知產品單價P(萬元)與產品件數x滿足:p2=![]() ,生產100件這樣的產品單價為50萬元.
,生產100件這樣的產品單價為50萬元.
(1)設產量為x件時,總利潤為L(x)(萬元),求L(x)的解析式;
(2)產量x定為多少件時總利潤L(x)(萬元)最大?并求最大值(精確到1萬元).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解中學生對交通安全知識的掌握情況,從農村中學和城鎮中學各選取100名同學進行交通安全知識競賽.下圖1和圖2分別是對農村中學和城鎮中學參加競賽的學生成績按![]() ,
,![]() ,
,![]() ,
,![]() 分組,得到的頻率分布直方圖.
分組,得到的頻率分布直方圖.
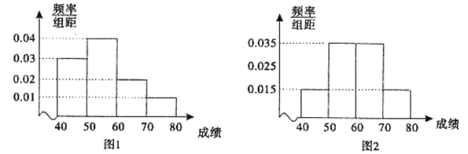
(Ⅰ)分別估算參加這次知識競賽的農村中學和城鎮中學的平均成績;
(Ⅱ)完成下面![]() 列聯表,并回答是否有
列聯表,并回答是否有![]() 的把握認為“農村中學和城鎮中學的學生對交通安全知識的掌握情況有顯著差異”?
的把握認為“農村中學和城鎮中學的學生對交通安全知識的掌握情況有顯著差異”?
成績小于60分人數 | 成績不小于60分人數 | 合計 | |
農村中學 | |||
城鎮中學 | |||
合計 |
附:![]()
臨界值表:
| 0.10 | 0.05 | 0.010 |
| 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法正確的是( )
A.若冪函數![]() 的圖象過點
的圖象過點![]() ,則
,則![]()
B.命題![]() :“
:“![]() ,
,![]() ”,則
”,則![]() 的否定為“
的否定為“![]() ,
,![]() ”
”
C.“![]() ”是“
”是“![]() ”的充分不必要條件
”的充分不必要條件
D.若![]() 與
與![]() 是相互獨立事件,則
是相互獨立事件,則![]() 與
與![]() 也是相互獨立事件
也是相互獨立事件
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com