考點:利用導數研究曲線上某點切線方程,利用導數求閉區間上函數的最值,不等式比較大小
專題:轉化思想,導數的綜合應用,不等式的解法及應用
分析:(Ⅰ)把a=2代入函數f(x)的解析式,構造函數g(x)=f(x)-(6x
2+6x),求導得到其最大值為g(0)=0,從而得到f(x)與6x
2+6x的大小;
(Ⅱ)首先證明函數f(x)的圖象與直線y=6x的一個公共點時a的值為2,當a=2時構造函數h(x)=
f()-=lnx+-1-,求導后放縮得到
h′(x)≤-=,然后記分子為p(x),二次求導后得到p(x)說明存在x
0∈(1,3),使p′(x
0)=0,且在(1,x
0)上遞減,在(x
0,3)上遞增,再由又p(1)=0,p(3)=0,說明x∈[1,3]時,p(x)
max=0,x∈(1,3)時恒有p(x)<0,進而恒有h′(x)<0,h(x)在(1,3)上遞減,則(x+3)f(
)<6x-6成立.
解答:
(Ⅰ)解:a=2時,f(x)=2x+2ln(2x+1)(x>-
),
記g(x)=f(x)-(6x
2+6x),則
g′(x)=f′(x)-(12x+6)=-4•,
當
x∈(-,0)時,g′(x)>0;當x∈(0,+∞)時,g′(x)<0,
∴g(x)在x=0時取得極大值,也是最大值為g(0)=0,
則g(x)=f(x)-(6x
2+6x)≤g(0)=0,
即f(x)≤6x
2+6x;
(Ⅱ)證明:O(0,0)是函數f(x)的圖象與直線y=6x的一個公共點,
f′(x)=a+,f′(0)=3a.
若函數y=f(x)在(0,0)處相切,則3a=6,解得a=2,
當函數f(x)的圖象與直線y=6x不在(0,0)處相切時,設切點為P(x
0,y
0),
則y(x
0)=ax
0+2ln(ax
0+1)=6x
0,且
y′(x0)=a+=6,
聯立消去x
0得,
2ln+-3=0,
設
φ(a)=2ln+-3,則
φ′(a)=2••-=,
當a∈(1,2)時,φ′(a)<0;當a∈(2,6)時,φ′(a)>0,
∴φ(a)在a=2時有最小值為φ(2)=0,
∴函數φ(a)有唯一零點a=2.
即函數f(x)的圖象與直線y=6x相切,則a=2.
由a=2,得
f()=+lnx-1,
記h(x)=
f()-=lnx+-1-,
則
h′(x)=+-,
∵x∈(1,3),∴
+===≤,
∴
h′(x)≤-=.
又記p(x)=(x+5)(x+3)
2-96x=x
3+11x
2-57x+45,
則p′(x)=3x
2+22x-57,p′(1)=-320,
說明存在x
0∈(1,3),使p′(x
0)=0.
∵p′(x)是二次函數,則x∈(1,x
0)時,p′(x)<0;
x∈(x
0,3)時,p′(x)>0,
∴p(x)在(1,x
0)上遞減,在(x
0,3)上遞增.
又p(1)=96-96=0,p(3)=288-288=0,
則x∈[1,3]時,p(x)
max=0,x∈(1,3)時恒有p(x)<0,
進而恒有h′(x)<0,h(x)在(1,3)上遞減.
故x∈(1,3)時恒有h(x)<h(1)=0,
即(x+3)f(
)<6x-6.
點評:本題考查了利用導數研究過曲線上某點處的切線方程,考查了利用導數求函數的最值,對于(Ⅱ)的證明,對h(x)求導后的放縮是該題的難點和關鍵,體現了數學轉化思想方法,本題對于學生的邏輯思維能力要求過高,同時要求考生具有較強的計算能力,是難度較大的題目.



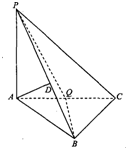 在三棱錐P-ABC中,PA⊥底面ABC,AD⊥平面PBC,其垂足D落在直線PB上,
在三棱錐P-ABC中,PA⊥底面ABC,AD⊥平面PBC,其垂足D落在直線PB上,