
【題目】已知橢圓![]() 的左右焦點分別為
的左右焦點分別為![]() ,
,![]() ,以
,以![]() ,
,![]() ,
,![]() 和
和![]() 為頂點的梯形的高為
為頂點的梯形的高為![]() ,面積為
,面積為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)設![]() ,
,![]() 為橢圓
為橢圓![]() 上的任意兩點,若直線
上的任意兩點,若直線![]() 與圓
與圓![]() 相切,求
相切,求![]() 面積的取值范圍.
面積的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由梯形![]() 的高求出
的高求出![]() ,由梯形
,由梯形![]() 的面積,建立關于
的面積,建立關于![]() 方程,結合
方程,結合![]() 關系,即可求出橢圓標準方程;
關系,即可求出橢圓標準方程;
(2)設直線![]() 的方程為:
的方程為:![]() ,利用直線與圓
,利用直線與圓![]() 相切,得到
相切,得到![]() 關系,直線方程與橢圓方程聯立,設
關系,直線方程與橢圓方程聯立,設![]() ,
,![]() ,得出
,得出![]() 關系,由相交弦長公式,求出
關系,由相交弦長公式,求出![]() 關于
關于![]() 的函數,根據函數特征,求出其范圍,再由
的函數,根據函數特征,求出其范圍,再由![]() ,即可求出結論.
,即可求出結論.
(1)由題意,得![]() ,且
,且![]() ,
,
∴![]() ,又
,又![]() ,解得
,解得![]() ,
,![]() .
.
∴橢圓![]() 的方程為
的方程為![]() .
.
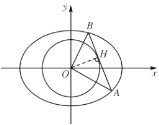
(2)如圖,設![]() ,
,![]() ,
,
當圓![]() 的切線
的切線![]() 的斜率存在時,設
的斜率存在時,設![]() 的方程為:
的方程為:![]() ,
,
切點為![]() ,連結
,連結![]() ,則
,則![]() .
.
因為![]() 與圓
與圓![]() 相切,
相切,
所以![]() ,所以
,所以![]() .
.
聯立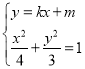 ,整理得
,整理得![]() .
.
![]()
![]()
所以![]() ,
,![]() .
.
又![]()
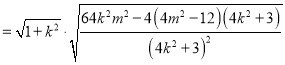
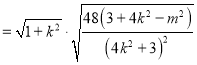
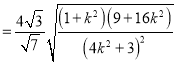
![]() .
.
①若![]() 時,
時,
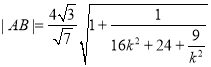 .
.
因為![]() ,
,
當且僅當![]() 時,“
時,“![]() ”成立.
”成立.
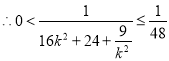
所以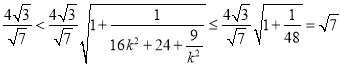
即![]() .
.
②當![]() 時,
時,![]() ,所以
,所以![]() .
.
又![]() ,
,
所以![]() .
.
當圓![]() 的切線斜率不存在時,則
的切線斜率不存在時,則![]() 的方程為
的方程為![]() 或
或![]() .
.
此時![]() ,
,![]() 的坐標分別為
的坐標分別為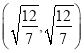 ,
, 或
或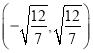 ,
,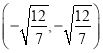 .此時
.此時![]() .
.
綜上,![]() 面積的取值范圍為
面積的取值范圍為![]() .
.


 小學生10分鐘口算測試100分系列答案
小學生10分鐘口算測試100分系列答案科目:高中數學 來源: 題型:
【題目】為了貫徹落實黨中央對新冠肺炎疫情防控工作的部署和要求,堅決防范疫情向校園蔓延,切實保障廣大師生身體健康和生命的安全,教育主管部門決定通過電視頻道、網絡平臺等多種方式實施線上教育教學工作.某教育機構為了了解人們對其數學網課授課方式的滿意度,從經濟不發達的A城市和經濟發達的B城市分別隨機調查了20個用戶,得到了一個用戶滿意度評分的樣本,并繪制出莖葉圖如下:
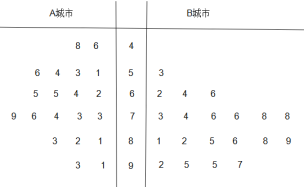
若評分不低于80分,則認為該用戶對此教育機構授課方式“認可”,否則認為該用戶對此教育機構授課方式“不認可”.
(Ⅰ)請根據此樣本完成下列2×2列聯表,并據此列聯表分析,能否有95%的把握認為城市經濟狀況與該市的用戶認可該教育機構授課方式有關?
認可 | 不認可 | 合計 | |
A城市 | |||
B城市 | |||
合計 |
(Ⅱ)在樣本A,B兩個城市對此教育機構授課方式“認可”的用戶中按分層抽樣的方法抽取6人,若在此6人中任選2人參加數學競賽,求A城市中至少有1人參加的概率.
參考公式: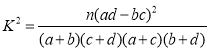 ,其中
,其中![]() .
.
參考數據:
| 0.10 | 0.05 | 0.025 |
| 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,三棱柱![]() 的底面是等邊三角形,
的底面是等邊三角形,![]() 在底面ABC上的射影為△ABC的重心G.
在底面ABC上的射影為△ABC的重心G.
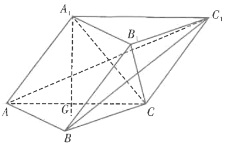
(1)已知![]() ,證明:平面
,證明:平面![]() 平面
平面![]() ;
;
(2)已知平面![]() 與平面ABC所成的二面角為60°,G到直線AB的距離為a,求銳二面角
與平面ABC所成的二面角為60°,G到直線AB的距離為a,求銳二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() 過拋物線
過拋物線![]() 的焦點,且與該拋物線交于
的焦點,且與該拋物線交于![]() ,
,![]() 兩點,若線段
兩點,若線段![]() 的長是16,
的長是16,![]() 的中點到
的中點到![]() 軸的距離是6,
軸的距離是6,![]() 是坐標原點,則( ).
是坐標原點,則( ).
A.拋物線![]() 的方程是
的方程是![]() B.拋物線的準線方程是
B.拋物線的準線方程是![]()
C.直線![]() 的方程是
的方程是![]() D.
D.![]() 的面積是
的面積是![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知過橢圓![]() 的四個頂點與坐標軸垂直的四條直線圍成的矩形
的四個頂點與坐標軸垂直的四條直線圍成的矩形![]() (
(![]() 是第一象限內的點)的面積為
是第一象限內的點)的面積為![]() ,且過橢圓
,且過橢圓![]() 的右焦點
的右焦點![]() 的傾斜角為
的傾斜角為![]() 的直線過點
的直線過點![]() .
.
(1)求橢圓![]() 的標準方程
的標準方程
(2)若射線![]() 與橢圓
與橢圓![]() 的交點分別為
的交點分別為![]() .當它們的斜率之積為
.當它們的斜率之積為![]() 時,試問
時,試問![]() 的面積是否為定值?若為定值,求出此定值;若不為定值,說明理由.
的面積是否為定值?若為定值,求出此定值;若不為定值,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解運動健身減肥的效果,某健身房調查了20名肥胖者,測量了他們的體重(單位:千克).健身之前他們的體重情況如三維餅圖(1)所示,經過半年的健身后,他們的體重情況如三維餅圖(2)所示,對比健身前后,關于這20名肥胖者,下面結論正確的是( )
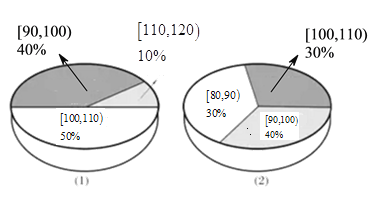
A.他們健身后,體重在區間![]() 內的人數不變
內的人數不變
B.他們健身后,體重在區間![]() 內的人數減少了2個
內的人數減少了2個
C.他們健身后,體重在區間![]() 內的肥胖者體重都有減輕
內的肥胖者體重都有減輕
D.他們健身后,這20位肥胖著的體重的中位數位于區間![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com