
分析 (1)求得拋物線的焦點坐標,則c=$\sqrt{3}$,將點代入橢圓方程,即可求得a和b的值,即可求得橢圓方程;
(2)設直線l的方程,代入橢圓方程,根據韋達定理及中點坐標,求得PQ的中點,利用中點坐標及中點坐標,根據二次函數的性質,即可求得△OPQ面積的最大值.
解答 解:(1)拋物線${y^2}=4\sqrt{3}x$的焦點為$(\sqrt{3},0)$,故得$c=\sqrt{3}$,
所以a2=b2+3,因點$(\sqrt{3},\frac{1}{2})$在橢圓C上,
∴$\frac{3}{a^2}+\frac{1}{{4{b^2}}}=1$,解得a2=4,b2=1,
∴橢圓C的方程為$\frac{x^2}{4}+{y^2}=1$;
(2)設P(x1,y1),Q(x2,y2)的中點為(x0,y0),
將直線y=kx+m(k≠0)代入$\frac{x^2}{4}+{y^2}=1$,得(1+4k2)x2+8kmx+4m2-4=0,
∴△=16(1+4k2-m2)>0,則${x_0}=\frac{1}{2}({x_1}+{x_2})=-\frac{4km}{{1+4{k^2}}}$,${y_0}=\frac{1}{2}({y_1}+{y_2})=-\frac{m}{{1+4{k^2}}}$,
因為(-1,0)是以PQ為對角線的菱形的一頂點,且不在橢圓上,
∴$\frac{{{y_0}-0}}{{{x_0}+1}}=-\frac{1}{k}$,即3km=1+4k2,解得${k^2}>\frac{1}{5}$,設O到直線的距離為$d=\frac{m}{{\sqrt{1+{k^2}}}}$,
則$S=\frac{1}{2}d|PQ|=\frac{1}{2}×\frac{m}{{\sqrt{1+{k^2}}}}×$$\frac{{\sqrt{1+{k^2}}•\sqrt{16(1+4{k^2}-{m^2})}}}{{1+4{k^2}}}=\frac{2}{9}\sqrt{20+\frac{1}{k^2}-\frac{1}{k^4}}$,
當$\frac{1}{k^2}=\frac{1}{2}$,即$k=±\sqrt{2}$時,三角形面積最大為1.
∴△OPQ面積的最大值1.
點評 本題考查橢圓及拋物線的性質,直線與橢圓的位置關系,考查韋達定理及中點坐標公式,考查二次函數的性質,考查計算能力,屬于中檔題.


 名牌學校分層周周測系列答案
名牌學校分層周周測系列答案 黃岡海淀全程培優測試卷系列答案
黃岡海淀全程培優測試卷系列答案科目:高中數學 來源: 題型:選擇題
| A. | (-∞,-3)∪(0,3) | B. | (-2,0)∪(3,+∞) | C. | (-3,3) | D. | (-∞,-3)∪(3,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 下表提供了某公司技術升級后生產A產品過程中記錄的產量x(噸)與相應的成本y(萬元)的幾組對照數據:
下表提供了某公司技術升級后生產A產品過程中記錄的產量x(噸)與相應的成本y(萬元)的幾組對照數據:| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
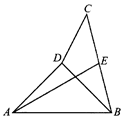 將正方形ABCD沿對角線BD折成直二面角后的圖形如圖所示,若E為線段BC的中點,則直線AE與平面ABD所成角的余弦為( )
將正方形ABCD沿對角線BD折成直二面角后的圖形如圖所示,若E為線段BC的中點,則直線AE與平面ABD所成角的余弦為( )| A. | $\frac{1}{4}$ | B. | $\frac{{\sqrt{6}}}{6}$ | C. | $\frac{{\sqrt{30}}}{6}$ | D. | $\frac{{\sqrt{15}}}{4}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | y=±3x | B. | $y=±\frac{1}{2}x$ | C. | y=±2x | D. | $y=±\frac{1}{3}x$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{{3\sqrt{5}}}{2}-1$ | B. | $\frac{{3\sqrt{3}}}{2}-1$ | C. | $2\sqrt{3}-1$ | D. | $\sqrt{10}-1$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com