
【題目】某公司為了對某種商品進行合理定價,需了解該商品的月銷售量![]() (單位:萬件)與月銷售單價
(單位:萬件)與月銷售單價![]() (單位:元/件)之間的關(guān)系,對近
(單位:元/件)之間的關(guān)系,對近![]() 個月的月銷售量
個月的月銷售量![]() 和月銷售單價
和月銷售單價![]()
![]() 數(shù)據(jù)進行了統(tǒng)計分析,得到一組檢測數(shù)據(jù)如表所示:
數(shù)據(jù)進行了統(tǒng)計分析,得到一組檢測數(shù)據(jù)如表所示:
月銷售單價 |
|
|
|
|
|
|
月銷售量 |
|
|
|
|
|
|
(1)若用線性回歸模型擬合![]() 與
與![]() 之間的關(guān)系,現(xiàn)有甲、乙、丙三位實習員工求得回歸直線方程分別為:
之間的關(guān)系,現(xiàn)有甲、乙、丙三位實習員工求得回歸直線方程分別為:![]() ,
,![]() 和
和![]() ,其中有且僅有一位實習員工的計算結(jié)果是正確的.請結(jié)合統(tǒng)計學的相關(guān)知識,判斷哪位實習員工的計算結(jié)果是正確的,并說明理由;
,其中有且僅有一位實習員工的計算結(jié)果是正確的.請結(jié)合統(tǒng)計學的相關(guān)知識,判斷哪位實習員工的計算結(jié)果是正確的,并說明理由;
(2)若用![]() 模型擬合
模型擬合![]() 與
與![]() 之間的關(guān)系,可得回歸方程為
之間的關(guān)系,可得回歸方程為![]() ,經(jīng)計算該模型和(1)中正確的線性回歸模型的相關(guān)指數(shù)
,經(jīng)計算該模型和(1)中正確的線性回歸模型的相關(guān)指數(shù)![]() 分別為
分別為![]() 和
和![]() ,請用
,請用![]() 說明哪個回歸模型的擬合效果更好;
說明哪個回歸模型的擬合效果更好;
(3)已知該商品的月銷售額為![]() (單位:萬元),利用(2)中的結(jié)果回答問題:當月銷售單價為何值時,商品的月銷售額預報值最大?(精確到
(單位:萬元),利用(2)中的結(jié)果回答問題:當月銷售單價為何值時,商品的月銷售額預報值最大?(精確到![]() )
)
參考數(shù)據(jù):![]() .
.
【答案】(1)甲;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根據(jù)數(shù)據(jù)知![]() 負相關(guān),排除乙,計算中心點驗證排除丙得到答案.
負相關(guān),排除乙,計算中心點驗證排除丙得到答案.
(2)![]() 越大,殘差平方和越小,擬合效果越好,
越大,殘差平方和越小,擬合效果越好,![]() ,得到答案.
,得到答案.
(3)![]() ,求導得到單調(diào)區(qū)間,得到答案.
,求導得到單調(diào)區(qū)間,得到答案.
(1)根據(jù)數(shù)據(jù)知![]() 負相關(guān),排除乙.
負相關(guān),排除乙.
![]() ,
,![]() .
.
代入驗證知,丙不滿足,故甲計算正確.
(2)![]() 越大,殘差平方和越小,擬合效果越好,
越大,殘差平方和越小,擬合效果越好,![]() ,
,
故選用![]() 更好.
更好.
(3)根據(jù)題意:![]() ,故
,故![]() .
.
令![]() ,則
,則![]() (舍去)或
(舍去)或![]() .
.
故當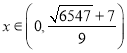 時,函數(shù)單調(diào)遞增,當
時,函數(shù)單調(diào)遞增,當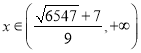 時,函數(shù)單調(diào)遞減.
時,函數(shù)單調(diào)遞減.
故當![]() 時,商品的月銷售額預報值最大.
時,商品的月銷售額預報值最大.


 小天才課時作業(yè)系列答案
小天才課時作業(yè)系列答案 一課四練系列答案
一課四練系列答案 黃岡小狀元滿分沖刺微測驗系列答案
黃岡小狀元滿分沖刺微測驗系列答案 新輔教導學系列答案
新輔教導學系列答案 陽光同學一線名師全優(yōu)好卷系列答案
陽光同學一線名師全優(yōu)好卷系列答案科目:高中數(shù)學 來源: 題型:
【題目】某企業(yè)生產(chǎn)甲、乙兩種產(chǎn)品均需用A,B兩種原料,已知生產(chǎn)1噸每種產(chǎn)品所需原料及每天原料的可用限額如表所示.如果生產(chǎn)1噸甲、乙產(chǎn)品可獲利潤分別為3萬元、4萬元,則該企業(yè)每天可獲得的最大利潤為( )
甲 | 乙 | 原料限額 | |
A/噸 | 3 | 2 | 12 |
B/噸 | 1 | 2 | 8 |
A.15萬元B.16萬元C.17萬元D.18萬元
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知橢圓E:
中,已知橢圓E:![]() 的離心率是
的離心率是![]() ,短軸長為2,若點A,B分別是橢圓E的左右頂點,動點
,短軸長為2,若點A,B分別是橢圓E的左右頂點,動點![]() ,
,![]() ,直線
,直線![]() 交橢圓E于P點.
交橢圓E于P點.
(1)求橢圓E的方程
(2)①求證:![]() 是定值;
是定值;
②設(shè)![]() 的面積為
的面積為![]() ,四邊形
,四邊形![]() 的面積為
的面積為![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】三棱錐![]() 中,
中,![]() ,△
,△![]() 為等邊三角形,二面角
為等邊三角形,二面角![]() 的余弦值為
的余弦值為![]() ,當三棱錐的體積最大時,其外接球的表面積為
,當三棱錐的體積最大時,其外接球的表面積為![]() .則三棱錐體積的最大值為( )
.則三棱錐體積的最大值為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖是一“T”型水渠的平面視圖(俯視圖),水渠的南北方向和東西方向軸截面均為矩形,南北向渠寬為4m,東西向渠寬![]() m(從拐角處,即圖中
m(從拐角處,即圖中![]() ,
,![]() 處開始).假定渠內(nèi)的水面始終保持水平位置(即無高度差).
處開始).假定渠內(nèi)的水面始終保持水平位置(即無高度差).
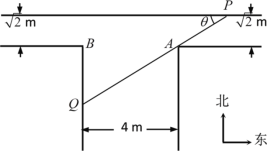
(1)在水平面內(nèi),過點![]() 的一條直線與水渠的內(nèi)壁交于
的一條直線與水渠的內(nèi)壁交于![]() ,
,![]() 兩點,且與水渠的一邊的夾角為
兩點,且與水渠的一邊的夾角為![]() ,將線段
,將線段![]() 的長度
的長度![]() 表示為
表示為![]() 的函數(shù);
的函數(shù);
(2)若從南面漂來一根長為7m的筆直的竹竿(粗細不計),竹竿始終浮于水平面內(nèi),且不發(fā)生形變,問:這根竹竿能否從拐角處一直漂向東西向的水渠(不會卡住)?請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】各項為正數(shù)的數(shù)列![]() 如果滿足:存在實數(shù)
如果滿足:存在實數(shù)![]() ,對任意正整數(shù)n,
,對任意正整數(shù)n,![]() 恒成立,且存在正整數(shù)n,使得
恒成立,且存在正整數(shù)n,使得![]() 或
或![]() 成立,則稱數(shù)列
成立,則稱數(shù)列![]() 為“緊密數(shù)列”,k稱為“緊密數(shù)列”
為“緊密數(shù)列”,k稱為“緊密數(shù)列”![]() 的“緊密度”.已知數(shù)列
的“緊密度”.已知數(shù)列![]() 的各項為正數(shù),前n項和為
的各項為正數(shù),前n項和為![]() ,且對任意正整數(shù)n,
,且對任意正整數(shù)n,![]() (A,B,C為常數(shù))恒成立.
(A,B,C為常數(shù))恒成立.
(1)當![]() ,
,![]() ,
,![]() 時,
時,
①求數(shù)列![]() 的通項公式;
的通項公式;
②證明數(shù)列![]() 是“緊密度”為3的“緊密數(shù)列”;
是“緊密度”為3的“緊密數(shù)列”;
(2)當![]() 時,已知數(shù)列
時,已知數(shù)列![]() 和數(shù)列
和數(shù)列![]() 都為“緊密數(shù)列”,“緊密度”分別為
都為“緊密數(shù)列”,“緊密度”分別為![]() ,
,![]() ,且
,且![]() ,
,![]() ,求實數(shù)B的取值范圍.
,求實數(shù)B的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】函數(shù)![]() 的定義域為
的定義域為![]() ,并滿足以下條件:①對任意
,并滿足以下條件:①對任意![]() ,有
,有![]() ;②對任意
;②對任意![]() ,有
,有![]() ;③
;③![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求證:![]() 在
在![]() 上是單調(diào)增函數(shù);
上是單調(diào)增函數(shù);
(Ⅲ)若![]() ,且
,且![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知![]() ,
,![]()
(1)求![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)若![]() ,
,![]() 在其公共點
在其公共點![]() 處切線相同,求實數(shù)a的值;
處切線相同,求實數(shù)a的值;
(3)記![]() ,若函數(shù)
,若函數(shù)![]() 存在兩個零點,求實數(shù)a的取值范圍.
存在兩個零點,求實數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知8支球隊中有3支弱隊,以抽簽方式將這8支球隊分為A、B兩組,每組4支.求:(1)A、B兩組中有一組恰有兩支弱隊的概率;
(2)A組中至少有兩支弱隊的概率.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com