
【題目】各項為正數的數列![]() 如果滿足:存在實數
如果滿足:存在實數![]() ,對任意正整數n,
,對任意正整數n,![]() 恒成立,且存在正整數n,使得
恒成立,且存在正整數n,使得![]() 或
或![]() 成立,則稱數列
成立,則稱數列![]() 為“緊密數列”,k稱為“緊密數列”
為“緊密數列”,k稱為“緊密數列”![]() 的“緊密度”.已知數列
的“緊密度”.已知數列![]() 的各項為正數,前n項和為
的各項為正數,前n項和為![]() ,且對任意正整數n,
,且對任意正整數n,![]() (A,B,C為常數)恒成立.
(A,B,C為常數)恒成立.
(1)當![]() ,
,![]() ,
,![]() 時,
時,
①求數列![]() 的通項公式;
的通項公式;
②證明數列![]() 是“緊密度”為3的“緊密數列”;
是“緊密度”為3的“緊密數列”;
(2)當![]() 時,已知數列
時,已知數列![]() 和數列
和數列![]() 都為“緊密數列”,“緊密度”分別為
都為“緊密數列”,“緊密度”分別為![]() ,
,![]() ,且
,且![]() ,
,![]() ,求實數B的取值范圍.
,求實數B的取值范圍.
【答案】(1)①![]() ②見解析;(2)
②見解析;(2)![]()
【解析】
(1)利用公式![]() 得到
得到![]() 是以首項為1,公差為2的等差數列,得到通項公式;計算
是以首項為1,公差為2的等差數列,得到通項公式;計算![]() 恒成立,得到證明.
恒成立,得到證明.
(2)根據遞推公式得到![]() 是以首項
是以首項![]() ,公比
,公比![]() 的等比數列,考慮
的等比數列,考慮![]() 和
和![]() 兩種情況,計算得到
兩種情況,計算得到![]() ,根據
,根據![]() 解得答案.
解得答案.
(1)①當![]() ,
,![]() ,
,![]() 時,
時,![]() ,
,
當![]() 時,
時,![]() ,
,
相減得:![]() ,
,
整理得:![]() ,因為
,因為![]() ,則
,則![]() ,
,
即有![]() ,當
,當![]() 時,
時,![]() ,則
,則![]() .
.
則![]() 是以首項為1,公差為2的等差數列,則
是以首項為1,公差為2的等差數列,則![]() .
.
②![]() ,得
,得![]() 隨著
隨著![]() 的增大而減小,
的增大而減小,
則對任意正整數n,![]() 恒成立,且存在
恒成立,且存在![]() ,使得
,使得![]() .
.
則數列![]() 是“緊密度”3的“緊密數列”.
是“緊密度”3的“緊密數列”.
(2)當![]() 時,
時,![]() ,
,![]() ,相減得:
,相減得:![]() ,
,
若![]() ,則上式右端中
,則上式右端中![]() ,與
,與![]() 矛盾;
矛盾;
若![]() ,則上式左端
,則上式左端![]() ,與
,與![]() 矛盾,則
矛盾,則![]() ,
,![]() .
.
則![]() 為常數,即
為常數,即![]() 是以首項
是以首項![]() ,公比
,公比![]() 的等比數列.
的等比數列.
因為數列![]() 為“緊密數列”,則
為“緊密數列”,則![]() , 所以
, 所以![]() ,又
,又![]() .
.
當![]() 時,
時,![]() ,對任意正整數
,對任意正整數![]() 恒成立,
恒成立,
且存在正整數![]() ,使得
,使得![]() ,所以數列
,所以數列![]() 的“緊密度”為
的“緊密度”為![]() ,
,
又![]() ,即
,即![]() ,
,
此時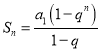 ,
,![]() 隨
隨![]() 的增大而減小,
的增大而減小,
所以![]() ,對任意正整數
,對任意正整數![]() 恒成立,
恒成立,
且當![]() 時,
時,![]() ,所以數列
,所以數列![]() 的“緊密度”為
的“緊密度”為![]() ,
,
則![]() ,與
,與![]() 矛盾,不成立;
矛盾,不成立;
當![]() 時,
時,![]() ,對任意正整數
,對任意正整數![]() 恒成立,
恒成立,
且存在正整數![]() ,使得
,使得![]() ,
,
則此時![]() 的“緊密度”為
的“緊密度”為![]() ,即
,即![]() .
.
而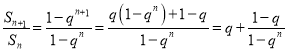 隨著
隨著![]() 的增大而減小,
的增大而減小,
則![]() 對任意正整數
對任意正整數![]() 恒成立,
恒成立,
且當![]() 時,
時,![]() ,則
,則![]() 的“緊密度”
的“緊密度”![]() ,即
,即![]() ,
,
故![]() ,即
,即![]() ,解得
,解得![]() .
.
綜上所述:實數![]() 的取值范圍為
的取值范圍為![]() .
.


 課堂全解字詞句段篇章系列答案
課堂全解字詞句段篇章系列答案 步步高口算題卡系列答案
步步高口算題卡系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓![]() ,右頂點
,右頂點![]() ,上頂點為B,左右焦點分別為
,上頂點為B,左右焦點分別為![]() ,且
,且![]() ,過點A作斜率為
,過點A作斜率為![]() 的直線l交橢圓于點D,交y軸于點E.
的直線l交橢圓于點D,交y軸于點E.
(1)求橢圓C的方程;
(2)設P為![]() 的中點,是否存在定點Q,對于任意的
的中點,是否存在定點Q,對于任意的![]() 都有
都有![]() ?若存在,求出點Q;若不存在,請說明理由.
?若存在,求出點Q;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為了對某種商品進行合理定價,需了解該商品的月銷售量![]() (單位:萬件)與月銷售單價
(單位:萬件)與月銷售單價![]() (單位:元/件)之間的關系,對近
(單位:元/件)之間的關系,對近![]() 個月的月銷售量
個月的月銷售量![]() 和月銷售單價
和月銷售單價![]()
![]() 數據進行了統計分析,得到一組檢測數據如表所示:
數據進行了統計分析,得到一組檢測數據如表所示:
月銷售單價 |
|
|
|
|
|
|
月銷售量 |
|
|
|
|
|
|
(1)若用線性回歸模型擬合![]() 與
與![]() 之間的關系,現有甲、乙、丙三位實習員工求得回歸直線方程分別為:
之間的關系,現有甲、乙、丙三位實習員工求得回歸直線方程分別為:![]() ,
,![]() 和
和![]() ,其中有且僅有一位實習員工的計算結果是正確的.請結合統計學的相關知識,判斷哪位實習員工的計算結果是正確的,并說明理由;
,其中有且僅有一位實習員工的計算結果是正確的.請結合統計學的相關知識,判斷哪位實習員工的計算結果是正確的,并說明理由;
(2)若用![]() 模型擬合
模型擬合![]() 與
與![]() 之間的關系,可得回歸方程為
之間的關系,可得回歸方程為![]() ,經計算該模型和(1)中正確的線性回歸模型的相關指數
,經計算該模型和(1)中正確的線性回歸模型的相關指數![]() 分別為
分別為![]() 和
和![]() ,請用
,請用![]() 說明哪個回歸模型的擬合效果更好;
說明哪個回歸模型的擬合效果更好;
(3)已知該商品的月銷售額為![]() (單位:萬元),利用(2)中的結果回答問題:當月銷售單價為何值時,商品的月銷售額預報值最大?(精確到
(單位:萬元),利用(2)中的結果回答問題:當月銷售單價為何值時,商品的月銷售額預報值最大?(精確到![]() )
)
參考數據:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() ,右頂點
,右頂點![]() ,上頂點為B,左右焦點分別為
,上頂點為B,左右焦點分別為![]() ,且
,且![]() ,過點A作斜率為
,過點A作斜率為![]() 的直線l交橢圓于點D,交y軸于點E.
的直線l交橢圓于點D,交y軸于點E.
(1)求橢圓C的方程;
(2)設P為![]() 的中點,是否存在定點Q,對于任意的
的中點,是否存在定點Q,對于任意的![]() 都有
都有![]() ?若存在,求出點Q;若不存在,請說明理由.
?若存在,求出點Q;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】斐波拉契數列,指的是這樣一個數列:1,1,2,3,5,8,13,21,…,在數學上,斐波拉契數列{an}定義如下:a1=a2=1,an=an﹣1+an﹣2(n≥3,n∈N),隨著n的增大,![]() 越來越逼近黃金分割
越來越逼近黃金分割![]() 0.618,故此數列也稱黃金分割數列,而以an+1、an為長和寬的長方形稱為“最美長方形”,已知某“最美長方形”的面積約為200平方厘米,則該長方形的長大約是( )
0.618,故此數列也稱黃金分割數列,而以an+1、an為長和寬的長方形稱為“最美長方形”,已知某“最美長方形”的面積約為200平方厘米,則該長方形的長大約是( )
A.20厘米B.19厘米C.18厘米D.17厘米
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】圖1是由![]() 和
和![]() 組成的一個平面圖形,其中
組成的一個平面圖形,其中![]() 是
是![]() 的高,
的高,![]() ,
,![]() ,
,![]() ,將
,將![]() 和
和![]() 分別沿著
分別沿著![]() ,
,![]() 折起,使得
折起,使得![]() 與
與![]() 重合于點B,G為
重合于點B,G為![]() 的中點,如圖2.
的中點,如圖2.
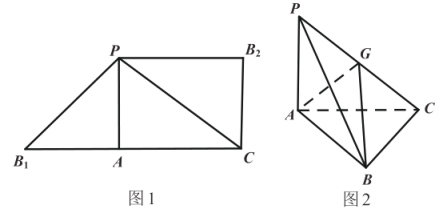
(1)求證:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求點C到平面
,求點C到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有人玩擲硬幣走跳棋的游戲,已知硬幣出現正反面為等可能性事件,棋盤上標有第0站,第1站,第2站,……,第100站.一枚棋子開始在第0站,棋手每擲一次硬幣,棋子向前跳動一次,若擲出正面,棋向前跳一站(從k到![]() ),若擲出反面,棋向前跳兩站(從k到
),若擲出反面,棋向前跳兩站(從k到![]() ),直到棋子跳到第99站(勝利大本營)或跳到第100站(失敗集中營)時,該游戲結束.設棋子跳到第n站概率為
),直到棋子跳到第99站(勝利大本營)或跳到第100站(失敗集中營)時,該游戲結束.設棋子跳到第n站概率為![]() .
.
(1)求![]() ,
,![]() ,
,![]() 的值;
的值;
(2)求證:![]() ,其中
,其中![]() ,
,![]() ;
;
(3)求![]() 及
及![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com