
【題目】斐波拉契數(shù)列,指的是這樣一個數(shù)列:1,1,2,3,5,8,13,21,…,在數(shù)學(xué)上,斐波拉契數(shù)列{an}定義如下:a1=a2=1,an=an﹣1+an﹣2(n≥3,n∈N),隨著n的增大,![]() 越來越逼近黃金分割
越來越逼近黃金分割![]() 0.618,故此數(shù)列也稱黃金分割數(shù)列,而以an+1、an為長和寬的長方形稱為“最美長方形”,已知某“最美長方形”的面積約為200平方厘米,則該長方形的長大約是( )
0.618,故此數(shù)列也稱黃金分割數(shù)列,而以an+1、an為長和寬的長方形稱為“最美長方形”,已知某“最美長方形”的面積約為200平方厘米,則該長方形的長大約是( )
A.20厘米B.19厘米C.18厘米D.17厘米
 云南師大附小一線名師提優(yōu)作業(yè)系列答案
云南師大附小一線名師提優(yōu)作業(yè)系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】一個多面體的直觀圖及三視圖如圖所示,其中M ,N 分別是AF、BC 的中點(diǎn)
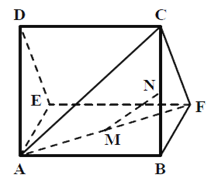
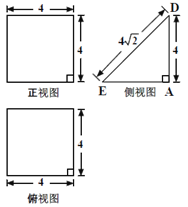
(1)求證:MN∥平面CDEF;
(2)求多面體A-CDEF的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】三棱錐![]() 中,
中,![]() ,△
,△![]() 為等邊三角形,二面角
為等邊三角形,二面角![]() 的余弦值為
的余弦值為![]() ,當(dāng)三棱錐的體積最大時,其外接球的表面積為
,當(dāng)三棱錐的體積最大時,其外接球的表面積為![]() .則三棱錐體積的最大值為( )
.則三棱錐體積的最大值為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】各項為正數(shù)的數(shù)列![]() 如果滿足:存在實(shí)數(shù)
如果滿足:存在實(shí)數(shù)![]() ,對任意正整數(shù)n,
,對任意正整數(shù)n,![]() 恒成立,且存在正整數(shù)n,使得
恒成立,且存在正整數(shù)n,使得![]() 或
或![]() 成立,則稱數(shù)列
成立,則稱數(shù)列![]() 為“緊密數(shù)列”,k稱為“緊密數(shù)列”
為“緊密數(shù)列”,k稱為“緊密數(shù)列”![]() 的“緊密度”.已知數(shù)列
的“緊密度”.已知數(shù)列![]() 的各項為正數(shù),前n項和為
的各項為正數(shù),前n項和為![]() ,且對任意正整數(shù)n,
,且對任意正整數(shù)n,![]() (A,B,C為常數(shù))恒成立.
(A,B,C為常數(shù))恒成立.
(1)當(dāng)![]() ,
,![]() ,
,![]() 時,
時,
①求數(shù)列![]() 的通項公式;
的通項公式;
②證明數(shù)列![]() 是“緊密度”為3的“緊密數(shù)列”;
是“緊密度”為3的“緊密數(shù)列”;
(2)當(dāng)![]() 時,已知數(shù)列
時,已知數(shù)列![]() 和數(shù)列
和數(shù)列![]() 都為“緊密數(shù)列”,“緊密度”分別為
都為“緊密數(shù)列”,“緊密度”分別為![]() ,
,![]() ,且
,且![]() ,
,![]() ,求實(shí)數(shù)B的取值范圍.
,求實(shí)數(shù)B的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】函數(shù)![]() 的定義域?yàn)?/span>
的定義域?yàn)?/span>![]() ,并滿足以下條件:①對任意
,并滿足以下條件:①對任意![]() ,有
,有![]() ;②對任意
;②對任意![]() ,有
,有![]() ;③
;③![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求證:![]() 在
在![]() 上是單調(diào)增函數(shù);
上是單調(diào)增函數(shù);
(Ⅲ)若![]() ,且
,且![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓O:x2+y2=3,直線PA與圓O相切于點(diǎn)A,直線PB垂直y軸于點(diǎn)B,且|PB|=2|PA|.
(1)求點(diǎn)P的軌跡E的方程;
(2)過點(diǎn)(1,0)且與x軸不重合的直線與軌跡E相交于P,Q兩點(diǎn),在x軸上是否存在定點(diǎn)D,使得x軸是∠PDQ的角平分線,若存在,求出D點(diǎn)坐標(biāo),若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() ,
,![]()
(1)求![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)若![]() ,
,![]() 在其公共點(diǎn)
在其公共點(diǎn)![]() 處切線相同,求實(shí)數(shù)a的值;
處切線相同,求實(shí)數(shù)a的值;
(3)記![]() ,若函數(shù)
,若函數(shù)![]() 存在兩個零點(diǎn),求實(shí)數(shù)a的取值范圍.
存在兩個零點(diǎn),求實(shí)數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系xOy中,直線l的參數(shù)方程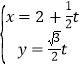 (t為參數(shù)),以坐標(biāo)原點(diǎn)為極點(diǎn),x軸正半軸為極軸建立極坐標(biāo)系,曲線C的極坐標(biāo)方程為:
(t為參數(shù)),以坐標(biāo)原點(diǎn)為極點(diǎn),x軸正半軸為極軸建立極坐標(biāo)系,曲線C的極坐標(biāo)方程為:![]() .
.
![]() Ⅰ
Ⅰ![]() 直線l的參數(shù)方程化為極坐標(biāo)方程;
直線l的參數(shù)方程化為極坐標(biāo)方程;
![]() Ⅱ
Ⅱ![]() 求直線l與曲線C交點(diǎn)的極坐標(biāo)
求直線l與曲線C交點(diǎn)的極坐標(biāo)![]() 其中
其中![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在二項式![]() 的展開式中,前三項系數(shù)的絕對值成等差數(shù)列。
的展開式中,前三項系數(shù)的絕對值成等差數(shù)列。
(1)求展開式的第四項;
(2)求展開式的常數(shù)項;
(3)求展開式中各項的系數(shù)和.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com