
【題目】已知圓O:x2+y2=3,直線PA與圓O相切于點A,直線PB垂直y軸于點B,且|PB|=2|PA|.
(1)求點P的軌跡E的方程;
(2)過點(1,0)且與x軸不重合的直線與軌跡E相交于P,Q兩點,在x軸上是否存在定點D,使得x軸是∠PDQ的角平分線,若存在,求出D點坐標(biāo),若不存在,說明理由.
【答案】(1)![]() (2)存在;定點D(4,0)
(2)存在;定點D(4,0)
【解析】
(1)設(shè)P(x,y),根據(jù)直線PA與圓O相切于點A,利用切線長公式得到|PA|2=x2+y2﹣3,|再根據(jù)直線PB垂直y軸于點B,得到|PB|2=x2,然后由|PB|=2|PA|求解.
(2)設(shè)直線l的方程為:x=my+1,與橢圓方程聯(lián)立,利用韋達定理得到![]() ,
,![]() ,代入kPD+kQD=0,化簡整理得
,代入kPD+kQD=0,化簡整理得![]() ,解得x0即可.
,解得x0即可.
(1)設(shè)P(x,y),因為直線PA與圓O相切于點A,
所以|PA|2=|PO|2﹣3=x2+y2﹣3,|
又因為直線PB垂直y軸于點B,
所以|PB|2=x2,
又因為|PB|=2|PA|
所以x2+y2﹣3=x2,
即x2=4(x2+y2﹣3),
化簡得![]() ,
,
∴點P的軌跡E的方程為:![]() ;
;
(2)設(shè)直線l的方程為:x=my+1,P(x1,y1),Q(x2,y2),
聯(lián)立方程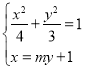 ,整理得:(4+3m2)y2+6my﹣9=0,
,整理得:(4+3m2)y2+6my﹣9=0,
∴![]() ,
,![]() ,
,
假設(shè)存在定點D(x0,0),使得x軸是∠PDQ的角平分線,則kPD+kQD=0,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
解得:x0=4,
所以存在定點D(4,0),使得x軸是∠PDQ的角平分線.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓方程為![]() .
.
(1)設(shè)橢圓的左右焦點分別為![]() 、
、![]() ,點
,點![]() 在橢圓上運動,求
在橢圓上運動,求![]() 的值;
的值;
(2)設(shè)直線![]() 和圓
和圓![]() 相切,和橢圓交于
相切,和橢圓交于![]() 、
、![]() 兩點,
兩點,![]() 為原點,線段
為原點,線段![]() 、
、![]() 分別和圓
分別和圓![]() 交于
交于![]() 、
、![]() 兩點,設(shè)
兩點,設(shè)![]() 、
、![]() 的面積分別為
的面積分別為![]() 、
、![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() ,右頂點
,右頂點![]() ,上頂點為B,左右焦點分別為
,上頂點為B,左右焦點分別為![]() ,且
,且![]() ,過點A作斜率為
,過點A作斜率為![]() 的直線l交橢圓于點D,交y軸于點E.
的直線l交橢圓于點D,交y軸于點E.
(1)求橢圓C的方程;
(2)設(shè)P為![]() 的中點,是否存在定點Q,對于任意的
的中點,是否存在定點Q,對于任意的![]() 都有
都有![]() ?若存在,求出點Q;若不存在,請說明理由.
?若存在,求出點Q;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】斐波拉契數(shù)列,指的是這樣一個數(shù)列:1,1,2,3,5,8,13,21,…,在數(shù)學(xué)上,斐波拉契數(shù)列{an}定義如下:a1=a2=1,an=an﹣1+an﹣2(n≥3,n∈N),隨著n的增大,![]() 越來越逼近黃金分割
越來越逼近黃金分割![]() 0.618,故此數(shù)列也稱黃金分割數(shù)列,而以an+1、an為長和寬的長方形稱為“最美長方形”,已知某“最美長方形”的面積約為200平方厘米,則該長方形的長大約是( )
0.618,故此數(shù)列也稱黃金分割數(shù)列,而以an+1、an為長和寬的長方形稱為“最美長方形”,已知某“最美長方形”的面積約為200平方厘米,則該長方形的長大約是( )
A.20厘米B.19厘米C.18厘米D.17厘米
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,某地區(qū)打算在一塊矩形地塊上修建一個牧場(ABCDEF圍成的封閉區(qū)域)用來養(yǎng)殖牛和羊,其中AF=1,AB=10,BC=4,CD=7(單位:百米),DEF是一段曲線形馬路.該牧場的核心區(qū)為等腰直角三角形MPQ所示區(qū)域,該區(qū)域用來養(yǎng)殖羊,其余區(qū)域養(yǎng)殖牛,且MP=PQ,牧場大門位于馬路DEF上的M處,一個觀察點P位于AB的中點處,為了能夠更好觀察動物的生活情況,現(xiàn)決定修建一條觀察通道,起點位于距離觀察點P處1百米的O點所示位置,終點位于Q處.如圖2所示,建立平面直角坐標(biāo)系,若![]() 滿足
滿足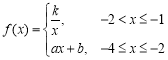 .
.
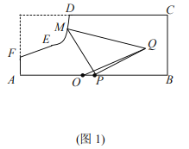
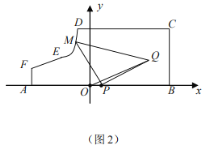
(1)求![]() 的解析式;
的解析式;
(2)求觀察通道OQ長度的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】圖1是由![]() 和
和![]() 組成的一個平面圖形,其中
組成的一個平面圖形,其中![]() 是
是![]() 的高,
的高,![]() ,
,![]() ,
,![]() ,將
,將![]() 和
和![]() 分別沿著
分別沿著![]() ,
,![]() 折起,使得
折起,使得![]() 與
與![]() 重合于點B,G為
重合于點B,G為![]() 的中點,如圖2.
的中點,如圖2.
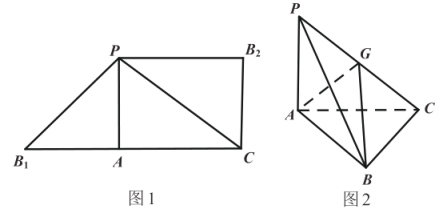
(1)求證:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求點C到平面
,求點C到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系xOy中,曲線C的參數(shù)方程為![]() (
(![]() 為參數(shù)),以坐標(biāo)原點為極點,x軸的正半軸為極軸建立極坐標(biāo)系,直線l的極坐標(biāo)方程為
為參數(shù)),以坐標(biāo)原點為極點,x軸的正半軸為極軸建立極坐標(biāo)系,直線l的極坐標(biāo)方程為![]() .
.
(1)求曲線C的極坐標(biāo)方程和直線l的直角坐標(biāo)方程;
(2)若射線![]() 與曲線C交于點A(不同于極點O),與直線l交于點B,求
與曲線C交于點A(不同于極點O),與直線l交于點B,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)甲、乙、丙三臺機器是否需要照顧相互之間沒有影響.已知在某1 h內(nèi),甲、乙都需要照顧的概率為0.05,甲、丙都需要照顧的概率為0.1,乙、丙都需要照顧的概率為0.125.
(1)求甲、乙、丙每臺機器在這1 h內(nèi)需要照顧的概率分別是多少?
(2)計算這1 h內(nèi)至少有一臺機器需要照顧的概率.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com