
【題目】已知函數![]() .
.
(1)若![]() ,求函數
,求函數![]() 在
在![]() 處的切線方程;
處的切線方程;
(2)令![]() ,討論函數
,討論函數![]() 的單調性;
的單調性;
(3)當![]() 時,
時,![]() ,求a的取值范圍.
,求a的取值范圍.
【答案】(1)![]() (2)詳見解析;(3)
(2)詳見解析;(3)![]()
【解析】
(1)利用公式![]() ,直接求切線方程;
,直接求切線方程;
(2)![]()
![]() ,首先求函數的導數,
,首先求函數的導數,![]() ,分類討論函數的單調性;
,分類討論函數的單調性;
(3)由(2)可知函數的單調性,結合![]() ,分
,分![]() ,
,![]() ,
,![]() ,三種情況討論函數的單調性,判斷是否能使
,三種情況討論函數的單調性,判斷是否能使![]() 時,
時,![]() 恒成立.
恒成立.
(1)當![]() 時,
時,![]()
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() 函數
函數![]() 在
在![]() 處的切線方程是
處的切線方程是![]() ;
;
(2)![]() ,
,
![]() ,
,![]()
當![]() 時,
時,![]() 恒成立,函數的單調遞減區間是
恒成立,函數的單調遞減區間是![]() ,無單調遞增區間;
,無單調遞增區間;
當![]() 時,
時,![]() ,
,
(ⅰ)![]() 時,即
時,即![]() 時,
時,![]() 的解集是
的解集是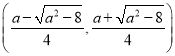 ,
,
![]() 的解集是
的解集是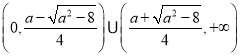 ,
,
所以函數的單調遞增區間是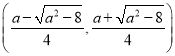 ,函數的單調遞減區間是
,函數的單調遞減區間是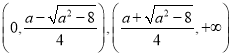 ;
;
(ⅱ)當![]() 時,即
時,即![]() 時,函數
時,函數![]() 恒成立,即函數的單調遞減區間是
恒成立,即函數的單調遞減區間是![]() ,無單調遞增區間;
,無單調遞增區間;
綜上可知,當![]() 時,函數的單調遞減區間是
時,函數的單調遞減區間是![]() ,無單調遞增區間;當
,無單調遞增區間;當![]() 時,函數的單調遞增區間是
時,函數的單調遞增區間是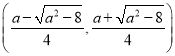 ,函數的單調遞減區間是
,函數的單調遞減區間是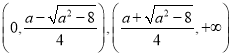 .
.
(3)![]() 時,
時,![]() 成立,
成立,
由(2)可知當![]() 時,
時,![]() 單調遞減,當
單調遞減,當![]() 時,
時,![]() 取得最大值,
取得最大值,![]() ,
,
(ⅰ)當![]() 時,
時,![]() ,
,![]()
![]() 恒成立,
恒成立,![]() 單調遞減,
單調遞減,![]() ,
,
![]() 當
當![]() 時,
時,![]() 恒成立,
恒成立,![]() ;
;
(ⅱ)當![]() 時,
時,![]() ,
,![]() 單調遞減,存在
單調遞減,存在![]() ,使
,使![]() ,即
,即![]() ,
,![]() ,
,![]() 單調遞增,當
單調遞增,當![]() 時,
時,![]() ,函數單調遞減,
,函數單調遞減,
![]()
![]() ,
,![]() 使
使![]() 不恒成立,故不成立;
不恒成立,故不成立;
(ⅲ)當![]() 時,
時,![]() ,由(2)可知
,由(2)可知![]() 的單調性,在
的單調性,在![]() 必存在區間
必存在區間![]() ,使函數
,使函數![]() ,即存在
,即存在![]() ,使
,使![]() 單調遞增,
單調遞增,
![]()
![]() ,
,![]() 使
使![]() 不恒成立,故不成立;
不恒成立,故不成立;
綜上可知:![]() .
.


 全優點練單元計劃系列答案
全優點練單元計劃系列答案科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是邊長為3的疋方形,側面
是邊長為3的疋方形,側面![]() 與底面
與底面![]() 垂直,過點
垂直,過點![]() 作
作![]() 的垂線,垂足為
的垂線,垂足為![]() ,且滿足
,且滿足![]() ,點
,點![]() 在棱
在棱![]() 上,
上,![]()
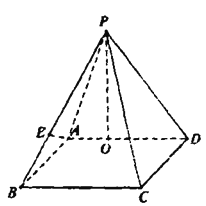
(1)當![]() 時,求直線
時,求直線![]() 與平面
與平面![]() 所成角的正弦值;
所成角的正弦值;
(2)當![]() 取何值時,二面角
取何值時,二面角![]() 的正弦值為
的正弦值為![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 是拋物線
是拋物線![]() 上的兩個點,點
上的兩個點,點![]() 的坐標為
的坐標為![]() ,直線
,直線![]() 的斜率為
的斜率為![]() .設拋物線
.設拋物線![]() 的焦點在直線
的焦點在直線![]() 的下方.
的下方.
(Ⅰ)求k的取值范圍;
(Ⅱ)設C為W上一點,且![]() ,過
,過![]() 兩點分別作W的切線,記兩切線的交點為
兩點分別作W的切線,記兩切線的交點為![]() . 判斷四邊形
. 判斷四邊形![]() 是否為梯形,并說明理由.
是否為梯形,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義在![]() 上的偶函數
上的偶函數![]() 滿足
滿足![]() ,且
,且![]() ,當
,當![]() 時,
時,![]() .已知方程
.已知方程![]() 在區間
在區間![]() 上所有的實數根之和為
上所有的實數根之和為![]() .將函數
.將函數![]() 的圖象向右平移
的圖象向右平移![]() 個單位長度,得到函數
個單位長度,得到函數![]() 的圖象,則
的圖象,則![]() __________,
__________,![]() __________.
__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,已知四邊形
中,已知四邊形![]() 是邊長為
是邊長為![]() 的正方形,點
的正方形,點![]() 在底面
在底面![]() 上的射影為底面
上的射影為底面![]() 的中心點
的中心點![]() ,點
,點![]() 在棱
在棱![]() 上,且
上,且![]() 的面積為1.
的面積為1.
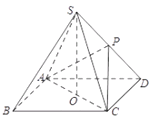
(1)若點![]() 是
是![]() 的中點,求證:平面
的中點,求證:平面![]() 平面
平面![]() ;
;
(2)在棱![]() 上是否存在一點
上是否存在一點![]() 使得二面角
使得二面角![]() 的余弦值為
的余弦值為![]() ?若存在,求出點
?若存在,求出點![]() 的位置;若不存在,說明理由.
的位置;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)若函數f(x)的圖象在點(2,f(2))處的切線方程為9x﹣y+b=0,求實數a,b的值;
(2)若a≤0,求f(x)的單調減區間;
(3)對一切實數a∈(0,1),求f(x)的極小值的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學舉行了一次“環保知識競賽”, 全校學生參加了這次競賽.為了了解本次競賽成績情況,從中抽取了部分學生的成績(得分取正整數,滿分為100分)作為樣本進行統計.請根據下面尚未完成并有局部污損的頻率分布表和頻率分布直方圖(如圖所示)解決下列問題:
![]()
| 分組 | 頻數 | 頻率 |
第1組 | [50,60) | 8 | 0 16 |
第2組 | [60,70) | a | ▓ |
第3組 | [70,80) | 20 | 0 40 |
第4組 | [80,90) | ▓ | 0 08 |
第5組 | [90,100] | 2 | b |
合計 | ▓ | ▓ |
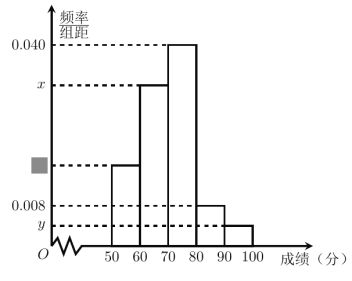
(1)求出![]() 的值;
的值;
(2)在選取的樣本中,從競賽成績是80分以上(含80分)的同學中隨機抽取2名同學到廣場參加環保知識的志愿宣傳活動
(ⅰ)求所抽取的2名同學中至少有1名同學來自第5組的概率;
(ⅱ)求所抽取的2名同學來自同一組的概率
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個三位數:個位、十位、百位上的數字依次為![]() ,
,![]() ,
,![]() ,當且僅當
,當且僅當![]() ,
,![]() 時,稱這樣的數為“凸數”(如243),現從集合
時,稱這樣的數為“凸數”(如243),現從集合![]() 中取出三個不同的數組成一個三位數,則這個三位數是“凸數”的概率為( )
中取出三個不同的數組成一個三位數,則這個三位數是“凸數”的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com