【題目】過雙曲線x2﹣ 
=1的右支上一點P，分別向圓C1：（x+4）2+y2=4和圓C2：（x﹣4）2+y2=1作切線，切點分別為M，N，則|PM|2﹣|PN|2的最小值為（ ）
A.10
B.13
C.16
D.19
【答案】B
【解析】解：圓C1：（x+4）2+y2=4的圓心為（﹣4，0），半徑為r1=2；圓C2：（x﹣4）2+y2=1的圓心為（4，0），半徑為r2=1，
設雙曲線x2﹣ 
=1的左右焦點為F1（﹣4，0），F2（4，0），
連接PF1 ， PF2 ， F1M，F2N，可得
|PM|2﹣|PN|2=（|PF1|2﹣r12）﹣（|PF2|2﹣r22）
=（|PF1|2﹣4）﹣（|PF2|2﹣1）
=|PF1|2﹣|PF2|2﹣3=（|PF1|﹣|PF2|）（|PF1|+|PF2|）﹣3
=2a（|PF1|+|PF2|﹣3=2（|PF1|+|PF2|）﹣3≥22c﹣3=28﹣3=13．
當且僅當P為右頂點時，取得等號，
即最小值13．
故選B．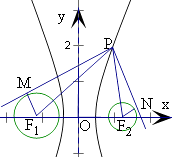
求得兩圓的圓心和半徑，設雙曲線x2﹣ =1的左右焦點為F1（﹣4，0），F2（4，0），連接PF1 ， PF2 ， F1M，F2N，運用勾股定理和雙曲線的定義，結合三點共線時，距離之和取得最小值，計算即可得到所求值．
學練快車道快樂假期暑假作業新疆人民出版社系列答案
浙大優學小學年級銜接導與練浙江大學出版社系列答案
小學暑假作業東南大學出版社系列答案
津橋教育暑假拔高銜接廣東人民出版社系列答案
波波熊暑假作業江西人民出版社系列答案科目：高中數學 來源： 題型：
【題目】已知f（x），g（x）分別是定義在R上的奇函數和偶函數，且f（x）+g（x）=3x ．
（1）求 f（x），g（x）；
（2）若對于任意實數t∈[0，1]，不等式f（2t）+ag（t）＜0恒成立，求實數a的取值范圍；
（3）若存在m∈[﹣2，﹣1]，使得不等式af（m）+g（2m）＜0成立，求實數a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】關于函數f（x）=2sin（3x﹣ 
），有下列命題：①其表達式可改寫為y=2cos（3x﹣ 
）；②y=f（x）的最小正周期為 
；③y=f（x）在區間（ 
， 
）上是增函數；④將函數y=2sin3x的圖象上所有點向左平行移動 個單位長度就得到函數y=f（x）的圖象．其中正確的命題的序號是（注：將你認為正確的命題序號都填上）．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列{an}是等比數列，首項a1=1，公比q＞0，其前n項和為Sn，且S1+a1，S3+a3，S2+a2成等差數列．
（Ⅰ）求數列{an}的通項公式；
（Ⅱ）若數列{bn}滿足
，Tn為數列{bn}的前n項和，若Tn≥m恒成立，求m的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】一條寬為
的兩平行河岸有村莊
和供電站
，村莊
與
的直線距離都是
， 
與河岸垂直，垂足為
現要修建電纜，從供電站
向村莊
供電．修建地下電纜、水下電纜的費用分別是
萬元
、
萬元
.
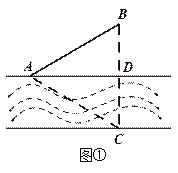
(1) 如圖①,已知村莊
與
原來鋪設有電纜
，現先從
處修建最短水下電纜到達對岸后后，再修建地下電纜接入原電纜供電，試求該方案總施工費用的最小值；
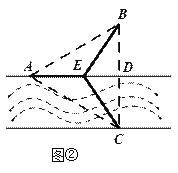
(2) 如圖②，點
在線段
上，且鋪設電纜的線路為
.若
，試用
表示出總施工費用
（萬元）的解析式，并求
的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】定義在（﹣1，1）上的函數f（x）滿足： 
，當x∈（﹣1，0）時，有f（x）＞0，且 
．設 
，則實數m與﹣1的大小關系為（ ）
A.m＜﹣1
B.m=﹣1
C.m＞﹣1
D.不確定
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=loga 
，（a＞0且a≠1）．
（1）判斷f（x）的奇偶性，并加以證明；
（2）是否存在實數m使得f（x+2）+f（m﹣x）為常數？若存在，求出m的值；若不存在，說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知命題p：x∈A，且A={x|a﹣1＜x＜a+1}，命題q：x∈B，且B={x|x2﹣4x+3≥0}
（Ⅰ）若A∩B=，A∪B=R，求實數a的值；
（Ⅱ）若p是q的充分條件，求實數a的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
