
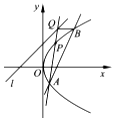
 已知直線l的方程為y=x+2,點P是拋物線y2=4x上到直線l距離最小的點,點A是拋物線上異于點P的點,直線AP與直線l交于點Q,過點Q與x軸平行的直線與拋物線y2=4x交于點B.
已知直線l的方程為y=x+2,點P是拋物線y2=4x上到直線l距離最小的點,點A是拋物線上異于點P的點,直線AP與直線l交于點Q,過點Q與x軸平行的直線與拋物線y2=4x交于點B.分析 (Ⅰ)利用點到直線的距離公式,求出最小值,然后求點P的坐標;
(Ⅱ)設點A的坐標為$({\frac{y_1^2}{4},{y_1}})$,顯然y1≠2.通過當y1=-2時,求出直線AP的方程為x=1;當y1≠-2時,求出直線AP的方程,然后求出Q的坐標,求出B點的坐標,解出直線AB的斜率,推出AB的方程,判斷直線AB恒過定點推出結果.
解答 解:(Ⅰ)設點P的坐標為(x0,y0),則$y_0^2=4{x_0}$,
所以,點P到直線l的距離$d=\frac{{|{{x_0}-{y_0}+2}|}}{{\sqrt{2}}}=\frac{{|{\frac{y_0^2}{4}-{y_0}+2}|}}{{\sqrt{2}}}=\frac{{|{{{({{y_0}-2})}^2}+4}|}}{{4\sqrt{2}}}≥\frac{{\sqrt{2}}}{2}$.
當且僅當y0=2時等號成立,此時P點坐標為(1,2).…(4分)
(Ⅱ)設點A的坐標為$({\frac{y_1^2}{4},{y_1}})$,顯然y1≠2.
當y1=-2時,A點坐標為(1,-2),直線AP的方程為x=1;可得B($\frac{9}{4}$,3),直線AB:y=4x-6;
當y1≠-2時,直線AP的方程為$y-2=\frac{{{y_1}-2}}{{\frac{y_1^2}{4}-1}}({x-1})$,
化簡得4x-(y1+2)y+2y1=0;
綜上,直線AP的方程為4x-(y1+2)y+2y1=0.
與直線l的方程y=x+2聯立,可得點Q的縱坐標為${y_Q}=\frac{{2{y_1}-8}}{{{y_1}-2}}$.
因為,BQ∥x軸,所以B點的縱坐標為${y_B}=\frac{{2{y_1}-8}}{{{y_1}-2}}$.
因此,B點的坐標為$({\frac{{{{({{y_1}-4})}^2}}}{{{{({{y_1}-2})}^2}}},\frac{{2{y_1}-8}}{{{y_1}-2}}})$.
當$\frac{{2{y_1}-8}}{{{y_1}-2}}≠-{y_1}$,即$y_1^2≠8$時,直線AB的斜率$k=\frac{{{y_1}-\frac{{2{y_1}-8}}{{{y_1}-2}}}}{{\frac{y_1^2}{4}-\frac{{{{({{y_1}-4})}^2}}}{{{{({{y_1}-2})}^2}}}}}=\frac{{4{y_1}-8}}{y_1^2-8}$.
所以直線AB的方程為$y-{y_1}=\frac{{4{y_1}-8}}{y_1^2-8}({x-\frac{y_1^2}{4}})$,
整理得$({y-2})y_1^2-4({x-2}){y_1}+8({x-y})=0$.
當x=2,y=2時,上式對任意y1恒成立,
此時,直線AB恒過定點(2,2),也在y=4x-6上,
當$y_1^2=8$時,直線AB的方程為x=2,仍過定點(2,2),
故符合題意的直線AB恒過定點(2,2).…(13分)
點評 本題主要考查拋物線的標準方程與幾何性質、直線方程、直線與拋物線的位置關系等基礎知識,考查推理論證能力、運算求解能力,考查數形結合、化歸與轉化、特殊與一般,分類與整合等數學思想.


 輕巧奪冠周測月考直通中考系列答案
輕巧奪冠周測月考直通中考系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
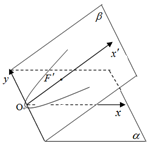 具有公共y軸的兩個直角坐標平面α和β所成的二面角α-y軸-β等于60°,已知β內的曲線C'的方程是y2=4x',曲線C'在α內的射影在平面α內的曲線方程為y2=2px,則p=1.
具有公共y軸的兩個直角坐標平面α和β所成的二面角α-y軸-β等于60°,已知β內的曲線C'的方程是y2=4x',曲線C'在α內的射影在平面α內的曲線方程為y2=2px,則p=1.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com