
分析 (1)求出函數(shù)的導(dǎo)數(shù),利用曲線f(x)在點(1,f(1))處的切線平行于x軸,求出a,然后判斷函數(shù)的單調(diào)性,求解函數(shù)的最小值即可.
(2)令$g(x)=f(x)-f(\frac{1}{x})$,化簡通過函數(shù)的導(dǎo)數(shù),判斷導(dǎo)函數(shù)的符號,然后通過x 的范圍,判斷兩個數(shù)的大小.
(3)要證xexlnx+ex>x3,即證:$lnx+\frac{1}{x}>\frac{x^2}{e^x}$,令$h(x)=\frac{x^2}{e^x}$,利用函數(shù)的導(dǎo)數(shù),判斷函數(shù)的單調(diào)性求出函數(shù)的最小值,即可證明結(jié)果.
解答 (本小題滿分12分)
解:(1)f'(x)=$\frac{a}{x}-\frac{1}{x^2}(x>0)$,根據(jù)題意知f'(1)=0,即a=1,∴$f(x)=lnx+\frac{1}{x}$,
…(2分)
∴f'(x)=$\frac{1}{x}-\frac{1}{x^2}=\frac{x-1}{x^2}$,∴當(dāng)0<x<1時,f'(x)<0,f(x)單調(diào)遞減;
當(dāng)x>1時,f'(x)>0,f(x)單調(diào)遞增;
∴f(x)min=f(1)=1. …(4分)
(2)令$g(x)=f(x)-f(\frac{1}{x})$=$lnx+\frac{1}{x}-[ln(\frac{1}{x})+x]$=$2lnx+\frac{1}{x}-x$,
$g'(x)=\frac{2}{x}-\frac{1}{x^2}-1=-\frac{{{{(x-1)}^2}}}{x^2}≤0$,
∴g(x)在(0,+∞)上單調(diào)遞減…(6分)
又∵g(1)=0∴當(dāng)0<x<1時,g(x)>g(1)=0,$f(x)>f(\frac{1}{x})$;
當(dāng)x>1時,g(x)<g(1)=0,$f(x)<f(\frac{1}{x})$;
當(dāng)x=1時,g(x)=0,$f(x)=f(\frac{1}{x})$.…(8分)
(3)要證xexlnx+ex>x3,即證:$lnx+\frac{1}{x}>\frac{x^2}{e^x}$…(10分)
令$h(x)=\frac{x^2}{e^x}$,即證∴f(x)>h(x),$h'(x)=\frac{{2x{e^x}-{e^x}{x^2}}}{{{e^{2x}}}}$=$\frac{{2x-{x^2}}}{e^x}$,
∴當(dāng)0<x<2時,h'(x)>0,h(x)單調(diào)遞增;
當(dāng)x>2時,h'(x)<0,h(x)單調(diào)遞減;∴h(x)max=h(2)=$\frac{4}{e^2}<1$,
又由(1)知f(x)min=1,∴f(x)≥1,∴f(x)>h(x),得證.…(12分)
附加題:(每小題(5分),共15分)
點評 本題考查函數(shù)的導(dǎo)數(shù)的綜合應(yīng)用,函數(shù)的單調(diào)性以及函數(shù)的最值的求法,考查轉(zhuǎn)化思想以及計算能力.


 小博士期末闖關(guān)100分系列答案
小博士期末闖關(guān)100分系列答案 名校名師培優(yōu)作業(yè)本加核心試卷系列答案
名校名師培優(yōu)作業(yè)本加核心試卷系列答案科目:高中數(shù)學(xué) 來源: 題型:解答題
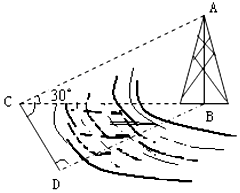 如圖,測量河對岸的塔高AB時,可以選與塔底B在同一水平面內(nèi)的兩個測點C與∠BCD=75°,∠BDC=60°,CD=20mD.現(xiàn)測得,并在點C測得塔頂A的仰角為30°,求塔高AB.
如圖,測量河對岸的塔高AB時,可以選與塔底B在同一水平面內(nèi)的兩個測點C與∠BCD=75°,∠BDC=60°,CD=20mD.現(xiàn)測得,并在點C測得塔頂A的仰角為30°,求塔高AB.查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
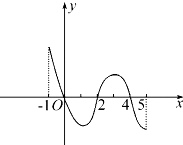 已知函數(shù)f(x)的定義域為[-1,5],部分對應(yīng)值如表:
已知函數(shù)f(x)的定義域為[-1,5],部分對應(yīng)值如表:| x | -1 | 0 | 2 | 4 | 5 |
| f(x) | 1 | 2 | 0 | 2 | 1 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com