
【題目】已知函數![]() ,g(x)=f(x)﹣3.
,g(x)=f(x)﹣3.
(1)判斷并證明函數g(x)的奇偶性;
(2)判斷并證明函數g(x)在(1,+∞)上的單調性;
(3)若f(m2﹣2m+7)≥f(2m2﹣4m+4)成立,求實數m的取值范圍.
【答案】(1) 奇函數,見解析 (2) 單調遞增,證明見解析(3) [﹣1,3].
【解析】
(1)函數g(x)為奇函數,計算得到![]() 得到證明.
得到證明.
(2)函數g(x)在(1,+∞)上單調遞增,設1<x1<x2,計算g(x1)﹣g(x2)<0得到證明.
(3)根據函數的單調性得到不等式m2﹣2m+7≥2m2﹣4m+4,計算得到答案.
(1)根據題意,g(x)為奇函數,
g(x)=f(x)﹣3![]() 3=﹣(
3=﹣(![]() ),
),
其定義域為{x|x≠﹣1且x≠0且x≠1},關于原點對稱,
則有g(﹣x)=﹣(![]() )=﹣g(x),則函數g(x)為奇函數;
)=﹣g(x),則函數g(x)為奇函數;
(2)根據題意,函數g(x)在(1,+∞)上的單調遞增,設1<x1<x2,
g(x1)﹣g(x2)=﹣[![]() ]+[
]+[![]() ]
]
=(x1﹣x2)[![]() ],
],
又由1<x1<x2,則g(x1)﹣g(x2)<0,則函數g(x)在(1,+∞)上的單調遞增,
(3)根據題意,g(x)在(1,+∞)上的單調遞增,
f(x)=g(x)+3在(1,+∞)上的單調遞增;
又由m2﹣2m+7=(m﹣1)2+6>1,2m2﹣4m+4=2(m﹣1)2+2>1
f(m2﹣2m+7)≥f(2m2﹣4m+4)![]() m2﹣2m+7≥2m2﹣4m+4,解可得:﹣1≤m≤3;
m2﹣2m+7≥2m2﹣4m+4,解可得:﹣1≤m≤3;
即m的取值范圍為[﹣1,3].


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】如圖所示,在四棱錐P—ABCD中,底面ABCD是矩形,側棱PA垂直于底面,E、F分別是AB、PC的中點,PA=AD.
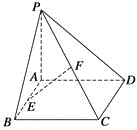
求證:(1)CD⊥PD;(2)EF⊥平面PCD.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為增進市民的環保意識,某市有關部門面向全體市民進行了一次環保知識的微信問卷測試活動,每位市民僅有一次參與問卷測試機會.通過抽樣,得到參與問卷測試的1000人的得分數據,制成頻率分布直方圖如圖所示.

(1)估計成績得分落在[86,100]中的概率.
(2)設這1000人得分的樣本平均值為![]() .
.
(i)求![]() (同一組數據用該區間的中點值作代表);
(同一組數據用該區間的中點值作代表);
(ii)有關部門為參與此次活動的市民贈送20元或10元的隨機話費,每次獲贈20元或10元的隨機話費的概率分別為![]() 和
和![]() .得分不低于
.得分不低于![]() 的可獲贈2次隨機話費,得分低于
的可獲贈2次隨機話費,得分低于![]() 的可獲贈1次隨機話費.求一位市民參與這次活動獲贈話費
的可獲贈1次隨機話費.求一位市民參與這次活動獲贈話費![]() 的平均估計值.
的平均估計值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩校分別有120名、100名學生參加了某培訓機構組織的自主招生培訓,考試結果出來以后,培訓機構為了進一步了解各校所培訓學生通過自主招生的情況,從甲校隨機抽取60人,從乙校隨機抽取50人進行分析,相關數據如下表.

(1)完成上面![]() 列聯表,并據此判斷是否有99%的把握認為自主招生通過情況與學生所在學校有關;
列聯表,并據此判斷是否有99%的把握認為自主招生通過情況與學生所在學校有關;
(2)現從甲、乙兩校通過的學生中采取分層抽樣的方法抽取5人,再從所抽取的5人種隨機抽取2人,求2人全部來自于乙校的概率.
參考公式:![]() .
.
參考數據:
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ax2+bx+c(a≠0),設函數y=[f(x)]2+pf(x)+q的零點所組成的集合為A,則以下集合不可能是A集合的序號為__.
①![]()
②![]()
③{﹣2,3,8}
④{﹣4,﹣1,0,2}
⑤{1,3,5,7}.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐![]() 中,底面 ABCD為矩形,側面為正三角形,且平面
中,底面 ABCD為矩形,側面為正三角形,且平面![]() 平面
平面 ![]() E 為 PD 中點,AD=2.
E 為 PD 中點,AD=2.
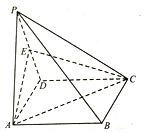
(1)證明平面AEC丄平面PCD;
(2)若二面角![]() 的平面角
的平面角![]() 滿足
滿足![]() ,求四棱錐
,求四棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年8月18日,舉世矚目的第18屆亞運會在印尼首都雅加達舉行,為了豐富亞運會志愿者的業余生活,同時鼓勵更多的有志青年加入志愿者行列,大會主辦方決定對150名志愿者組織一次有關體育運動的知識競賽(滿分120分)并計劃對成績前15名的志愿者進行獎勵,現將所有志愿者的競賽成績制成頻率分布直方圖,如圖所示,若第三組與第五組的頻數之和是第二組的頻數的3倍,試回答以下問題:
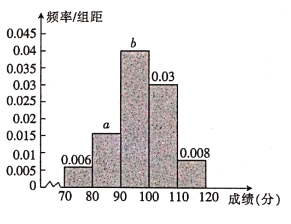
(1)求圖中![]() 的值;
的值;
(2)求志愿者知識競賽的平均成績;
(3)從受獎勵的15人中按成績利用分層抽樣抽取5人,再從抽取的5人中,隨機抽取2人在主會場服務,求抽取的這2人中其中一人成績在![]() 分的概率.
分的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com