
【題目】已知在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以
為參數),以![]() 軸的非負半軸為極軸,原點
軸的非負半軸為極軸,原點![]() 為極點建立極坐標系,兩種坐標系中取相同的長度單位,若直線
為極點建立極坐標系,兩種坐標系中取相同的長度單位,若直線![]() 和
和![]()
![]() 分別與曲線
分別與曲線![]() 相交于
相交于![]() 、
、![]() 兩點(
兩點(![]() ,
,![]() 兩點異于坐標原點).
兩點異于坐標原點).
(1)求曲線![]() 的普通方程與
的普通方程與![]() 、
、![]() 兩點的極坐標;
兩點的極坐標;
(2)求直線![]() 的極坐標方程及
的極坐標方程及![]() 的面積.
的面積.
科目:高中數學 來源: 題型:
【題目】有3名男生、4名女生,在下列不同條件下,求不同的排列方法總數.
(1)選5人排成一排;
(2)排成前后兩排,前排4人,后排3人;
(3)全體排成一排,甲不站排頭也不站排尾;
(4)全體排成一排,女生必須站在一起;
(5)全體排成一排,男生互不相鄰.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某單位擬建一個扇環面形狀的花壇(如圖所示),該扇環面是由以點![]() 為圓心的兩個同心圓弧和延長后通過點
為圓心的兩個同心圓弧和延長后通過點![]() 的兩條直線段圍成.按設計要求扇環面的周長為30米,其中大圓弧所在圓的半徑為10米.設小圓弧所在圓的半徑為
的兩條直線段圍成.按設計要求扇環面的周長為30米,其中大圓弧所在圓的半徑為10米.設小圓弧所在圓的半徑為![]() 米,圓心角為
米,圓心角為![]() (弧度).
(弧度).
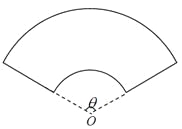
(1)求![]() 關于
關于![]() 的函數關系式;
的函數關系式;
(2)已知在花壇的邊緣(實線部分)進行裝飾時,直線部分的裝飾費用為4元/米,弧線部分的裝飾費用為9元/米.設花壇的面積與裝飾總費用的比為![]() ,求
,求![]() 關于
關于![]() 的函數關系式,并求出
的函數關系式,并求出![]() 為何值時,
為何值時, ![]() 取得最大值?
取得最大值?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(1)求證: ![]() .
.
(2)某同學在一次研究性學習中發現,以下五個式子的值都等于同一個常數:
sin213°+cos217°-sin13°cos17°;
sin215°+cos215°-sin15°cos15°;
sin218°+cos212°-sin18°cos12°;
sin2(-18°)+cos248°-sin(-18°)cos48°;
sin2(-25°)+cos255°-sin(-25°)cos55°.
①試從上述五個式子中選擇一個,求出這個常數;
②根據①的計算結果,將該同學的發現推廣為三角恒等式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() ,直線
,直線![]() .
.
(1)求證:對![]() 直線
直線![]() 與圓
與圓![]() 總有兩個不同的交點;
總有兩個不同的交點;
(2)是否存在實數![]() ,使得圓
,使得圓![]() 上有四個點到直線
上有四個點到直線![]() 的距離為
的距離為![]() ?若存在,求出
?若存在,求出![]() 的范圍,若不存在,說明理由.
的范圍,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以
為參數),以![]() 軸的非負半軸為極軸,原點
軸的非負半軸為極軸,原點![]() 為極點建立極坐標系,兩種坐標系中取相同的長度單位,若直線
為極點建立極坐標系,兩種坐標系中取相同的長度單位,若直線![]() 和
和![]()
![]() 分別與曲線
分別與曲線![]() 相交于
相交于![]() 、
、![]() 兩點(
兩點(![]() ,
,![]() 兩點異于坐標原點).
兩點異于坐標原點).
(1)求曲線![]() 的普通方程與
的普通方程與![]() 、
、![]() 兩點的極坐標;
兩點的極坐標;
(2)求直線![]() 的極坐標方程及
的極坐標方程及![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《周脾算經》有記載:一年有二十四個節氣,每個節氣晷(gui)長損益相同,晷是按照日影測定時刻的儀器,晷長即所測定的影子的長度,二十四節氣及晷長變化如圖所示,相鄰兩個節氣晷長變化量相同,周而復始,若冬至晷長最長是一丈三尺五寸,夏至晷長最短是一尺五寸,(一丈等于10尺,一尺等于10寸),則秋分節氣的晷長是( )
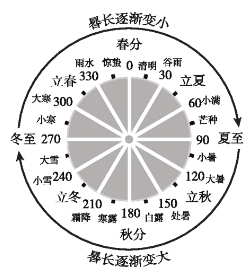
A.七尺五寸B.二尺五寸C.五尺五寸D.四尺五寸
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com