
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).以坐標原點為極點,
為參數).以坐標原點為極點,![]() 軸正半軸為極軸建立極坐標系,圓
軸正半軸為極軸建立極坐標系,圓![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 和圓
和圓![]() 的普通方程;
的普通方程;
(2)已知直線![]() 上一點
上一點![]() ,若直線
,若直線![]() 與圓
與圓![]() 交于不同兩點
交于不同兩點![]() ,求
,求![]() 的取值范圍.
的取值范圍.
科目:高中數學 來源: 題型:
【題目】某兒童樂園在“六一”兒童節推出了一項趣味活動.參加活動的兒童需轉動如圖所示的轉盤兩次,每次轉動后,待轉盤停止轉動時,記錄指針所指區域中的數.設兩次記錄的數分別為x,y.獎勵規則如下:

①若![]() ,則獎勵玩具一個;
,則獎勵玩具一個;
②若![]() ,則獎勵水杯一個;
,則獎勵水杯一個;
③其余情況獎勵飲料一瓶.
假設轉盤質地均勻,四個區域劃分均勻.小亮準備參加此項活動.
(Ⅰ)求小亮獲得玩具的概率;
(Ⅱ)請比較小亮獲得水杯與獲得飲料的概率的大小,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,則下列結論中正確的是( )
,則下列結論中正確的是( )
A. 將函數![]() 的圖象向左平移
的圖象向左平移![]() 個單位后得到函數
個單位后得到函數![]() 的圖象
的圖象
B. 函數![]() 圖象關于點
圖象關于點![]() 中心對稱
中心對稱
C. 函數![]() 的圖象關于
的圖象關于![]() 對稱
對稱
D. 函數![]() 在區間
在區間![]() 內單調遞增
內單調遞增
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設兩實數![]() 不相等且均不為
不相等且均不為![]() .若函數
.若函數![]() 在
在![]() 時,函數值
時,函數值![]() 的取值區間恰為
的取值區間恰為![]() ,就稱區間
,就稱區間![]() 為
為![]() 的一個“倒域區間”.已知函數
的一個“倒域區間”.已知函數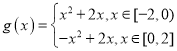 .
.
(1)求函數![]() 在
在![]() 內的“倒域區間”;
內的“倒域區間”;
(2)若函數![]() 在定義域
在定義域![]() 內所有“倒域區間”的圖象作為函數
內所有“倒域區間”的圖象作為函數![]() 的圖象,是否存在實數
的圖象,是否存在實數![]() ,使得
,使得![]() 與
與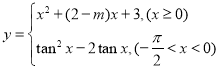 恰好有2個公共點?若存在,求出
恰好有2個公共點?若存在,求出![]() 的取值范圍:若不存在,請說明理由.
的取值范圍:若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,底面ABCD為正方形,平面PAD⊥平面ABCD,點M在線段PPD//平面MAC,PA=PD=![]() ,AB=4.
,AB=4.
(I)求證:M為PB的中點;
(II)求二面角B-PD-A的大小;
(III)求直線MC與平面BDP所成角的正弦值.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四面體ABCD中,O、E分別是BD、BC的中點,![]() ,
,![]() .
.
(1)求證:![]() 平面BCD;
平面BCD;
(2)求異面直線AB與CD所成角的余弦值;
(3)求點E到平面ACD的距離。

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】利用獨立性檢驗的方法調查高中生的寫作水平與離好閱讀是否有關,隨機詢問120名高中生是否喜好閱讀,利用2×2列聯表,由計算可得K2=4.236
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
參照附表,可得正確的結論是( )
A.有95%的把握認為“寫作水平與喜好閱讀有關”
B.有97.5%的把握認為“寫作水平與喜好閱讀有關”
C.有95%的把握認為“寫作水平與喜好閱讀無關”
D.有97.5%的把握認為“寫作水平與喜好閱讀無關”
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com