
【題目】已知函數 ![]() .
.
(1)證明: ![]() ;
;
(2)若對任意 ![]() ,不等式
,不等式 ![]() 恒成立,求實數
恒成立,求實數 ![]() 的取值范圍.
的取值范圍.
【答案】
(1)解:令 ![]() ,則
,則 ![]()
當 ![]() 所以
所以 ![]()
![]()
即 ![]() 在
在 ![]() 遞增;在
遞增;在 ![]() 遞減;
遞減;
所以 ![]() ,
, ![]()
(2)解:記 ![]() 則在
則在 ![]() 上,
上, ![]() ,
,![]()
①若 ![]() ,
, ![]() ,
, ![]() 時,
時, ![]() ,
, ![]() 單調遞增,
單調遞增, ![]() ,
,
這與 ![]() 上
上 ![]() 矛盾;
矛盾;
②若 ![]() ,
, ![]() ,
, ![]() 上
上 ![]() 遞增,而
遞增,而 ![]() ,這與
,這與 ![]() 上
上 ![]() 矛盾;
矛盾;
③若 ![]() ,
, ![]() ,
, ![]() 時
時 ![]() ,
, ![]() 單調遞減;
單調遞減; ![]() 時
時 ![]() 單遞增;
單遞增;
∴ ![]() ,即
,即 ![]() 恒成立;
恒成立;
④若 ![]() ,
, ![]() ,
, ![]() 時,
時, ![]() ,
, ![]() 單調遞增;
單調遞增; ![]() 時,
時, ![]() ,
, ![]() 單調遞減,∴
單調遞減,∴ ![]() ,這與
,這與 ![]() 上
上 ![]() 矛盾;
矛盾;
⑤若 ![]() ,
, ![]() ,
, ![]() 時,
時, ![]() ,
, ![]() 單調遞增;
單調遞增; ![]() 時,
時, ![]() ,
, ![]() 單調遞減,∴
單調遞減,∴ ![]() 這與
這與 ![]() 上
上 ![]() 矛盾.
矛盾.
綜上,實數 ![]() 的取值范圍是
的取值范圍是 ![]() .
.
【解析】(1)設一個新的函數g(x)= f ( x ) ( x 1 )然后求導,證明其在定義域內小于等于零.
(2)設一個新的函數h(x)=ax+![]() lnx,對a的取值進行討論,然后判斷當h=1時的值是否符合題意.
lnx,對a的取值進行討論,然后判斷當h=1時的值是否符合題意.


科目:高中數學 來源: 題型:
【題目】如圖直三棱柱 ![]() 中,
中, ![]() 為邊長為2的等邊三角形,
為邊長為2的等邊三角形, ![]() ,點
,點 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 分別是邊
分別是邊 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 的中點,動點
的中點,動點 ![]() 在四邊形
在四邊形 ![]() 內部運動,并且始終有
內部運動,并且始終有 ![]() 平面
平面 ![]() ,則動點
,則動點 ![]() 的軌跡長度為( )
的軌跡長度為( )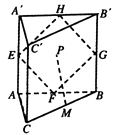
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,內角A,B,C的對邊分別為a,b,c,且a>b,a>c.△ABC的外接圓半徑為1, ![]() ,若邊BC上一點D滿足BD=2DC,且∠BAD=90°,則△ABC的面積為 .
,若邊BC上一點D滿足BD=2DC,且∠BAD=90°,則△ABC的面積為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某分公司經銷某種品牌產品,每件產品的成本為30元,并且每件產品須向總公司繳納a元(a為常數,2≤a≤5)的管理費,根據多年的統計經驗,預計當每件產品的售價為x元時,產品一年的銷售量為 ![]() (e為自然對數的底數)萬件,已知每件產品的售價為40元時,該產品一年的銷售量為500萬件.經物價部門核定每件產品的售價x最低不低于35元,最高不超過41元.
(e為自然對數的底數)萬件,已知每件產品的售價為40元時,該產品一年的銷售量為500萬件.經物價部門核定每件產品的售價x最低不低于35元,最高不超過41元.
(1)求分公司經營該產品一年的利潤L(x)萬元與每件產品的售價x元的函數關系式;
(2)當每件產品的售價為多少元時,該產品一年的利潤L(x)最大,并求出L(x)的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列判斷錯誤的是( )
A.若隨機變量 ![]() 服從正態分布
服從正態分布 ![]() ,則
,則 ![]() ;
;
B.若 ![]() 組數據
組數據 ![]() 的散點都在
的散點都在 ![]() 上,則相關系數
上,則相關系數 ![]() ;
;
C.若隨機變量 ![]() 服從二項分布:
服從二項分布: ![]() , 則
, 則 ![]() ;
;
D.![]() 是
是 ![]() 的充分不必要條件;
的充分不必要條件;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com