
【題目】在△ABC中,內角A,B,C的對邊分別為a,b,c,且a>b,a>c.△ABC的外接圓半徑為1, ![]() ,若邊BC上一點D滿足BD=2DC,且∠BAD=90°,則△ABC的面積為 .
,若邊BC上一點D滿足BD=2DC,且∠BAD=90°,則△ABC的面積為 .
科目:高中數學 來源: 題型:
【題目】設有下面四個命題
p1:若復數z滿足 ![]() ∈R,則z∈R;
∈R,則z∈R;
p2:若復數z滿足z2∈R,則z∈R;
p3:若復數z1 , z2滿足z1z2∈R,則z1= ![]() ;
;
p4:若復數z∈R,則 ![]() ∈R.
∈R.
其中的真命題為( )
A.p1 , p3
B.p1 , p4
C.p2 , p3
D.p2 , p4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正方體 ![]() 的棱長為1,
的棱長為1, ![]() 分別是棱
分別是棱 ![]() 的中點,過
的中點,過 ![]() 的平面與棱
的平面與棱 ![]() 分別交于點
分別交于點 ![]() .設
.設 ![]() ,
, ![]() .
.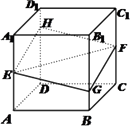
①四邊形 ![]() 一定是菱形;②
一定是菱形;② ![]() 平面
平面 ![]() ;③四邊形
;③四邊形 ![]() 的面積
的面積 ![]() 在區間
在區間 ![]() 上具有單調性;④四棱錐
上具有單調性;④四棱錐 ![]() 的體積為定值.
的體積為定值.
以上結論正確的個數是( )
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數f(x)=2x2-ln x在其定義域內的一個子區間(k-1,k+1)內不是單調函數,則實數k的取值范圍是( )
A.[1,+∞)
B.[1,2)
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知中心在原點 ![]() ,焦點在
,焦點在 ![]() 軸上,離心率為
軸上,離心率為 ![]() 的橢圓過點
的橢圓過點 ![]() .
.
(Ⅰ)求橢圓的方程;
(Ⅱ)設橢圓與 ![]() 軸的非負半軸交于點
軸的非負半軸交于點 ![]() ,過點
,過點 ![]() 作互相垂直的兩條直線,分別交橢圓于點
作互相垂直的兩條直線,分別交橢圓于點 ![]() ,
, ![]() 兩點,連接
兩點,連接 ![]() ,求
,求 ![]() 的面積的最大值.
的面積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com