
【題目】已知橢圓C中心在原點,焦點在坐標軸上,且該橢圓經過點( ![]() ,
, ![]() )和點
)和點 ![]() .求
.求
(1)橢圓C的方程;
(2)P,Q,M,N四點在橢圓C上,F1為負半軸上的焦點,直線PQ,MN都過F1且 ![]() ,求四邊形PMQN的面積最小值和最大值.
,求四邊形PMQN的面積最小值和最大值.
【答案】
(1)解:由題意,設橢圓的方程為mx2+ny2=1(m,n>0,m≠n),
代入點( ![]() ,
, ![]() )和點
)和點 ![]() ,可得
,可得
![]() m+
m+ ![]() n=1,
n=1, ![]() m+n=1,
m+n=1,
解得m=1,n= ![]() ,
,
即有橢圓方程為x2+ ![]() =1
=1
(2)解:由 ![]() ,可得直線PQ,MN垂直.
,可得直線PQ,MN垂直.
(ⅰ)若MN與PQ中一條斜率不存在,另一條斜率為0,
則四邊形PMQN的面積S= ![]() 2a
2a ![]() =2b2=2;
=2b2=2;
(ⅱ)若PQ與NM的斜率均存在,
設PQ:y=kx+1與橢圓方程聯立 ![]()
消去y可得(2+k2)x+2kx﹣1=0,則△=8(k2+1)>0,
設P(x1,y1),Q(x2,y2),
則x1+x2=﹣ ![]() ,x1x2=﹣
,x1x2=﹣ ![]() ,
,
∴|PQ|= ![]() |x1﹣x2|=
|x1﹣x2|= ![]()
![]() =2
=2 ![]()
![]() ;
;
同理可得|MN|=2 ![]()
![]() .
.
∴S= ![]() |PQ||MN|=4
|PQ||MN|=4 ![]() =
= 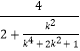 =
= 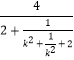 ,
,
由k2+ ![]() ≥2,得
≥2,得 ![]() ≤S<2.
≤S<2.
由(ⅰ)(ⅱ)知,Smin= ![]() ,Smax=2
,Smax=2
【解析】(1)由題意,設橢圓的方程為mx2+ny2=1(m,n>0,m≠n),代入兩點的坐標,建立方程組,從而可求橢圓的幾何量,即可求橢圓C的方程;(2)分斜率存在與存在分別討論,利用直線與橢圓聯立,根據韋達定理及弦長公式,確定面積的表達式,運用基本不等式可得最值,即可求得結論.


 中考利劍中考試卷匯編系列答案
中考利劍中考試卷匯編系列答案 教育世家狀元卷系列答案
教育世家狀元卷系列答案 黃岡課堂作業本系列答案
黃岡課堂作業本系列答案 單元加期末復習先鋒大考卷系列答案
單元加期末復習先鋒大考卷系列答案科目:高中數學 來源: 題型:
【題目】如圖,現要在邊長為100m的正方形ABCD內建一個交通“環島”.以正方形的四個頂點為圓心在四個角分別建半徑為xm(x不小于9)的扇形花壇,以正方形的中心為圓心建一個半徑為 ![]() m的圓形草地.為了保證道路暢通,島口寬不小于60m,繞島行駛的路寬均小于10m.
m的圓形草地.為了保證道路暢通,島口寬不小于60m,繞島行駛的路寬均小于10m. 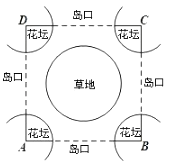
(1)求x的取值范圍;(運算中 ![]() 取1.4)
取1.4)
(2)若中間草地的造價為a元/m2 , 四個花壇的造價為 ![]() 元/m2 , 其余區域的造價為
元/m2 , 其余區域的造價為 ![]() 元/m2 , 當x取何值時,可使“環島”的整體造價最低?
元/m2 , 當x取何值時,可使“環島”的整體造價最低?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,點E為棱PC的中點. 
(1)證明:BE⊥DC;
(2)求直線BE與平面PBD所成角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知二次函數y=f(x)的圖象過坐標原點,其導函數f′(x)=6x﹣2,數列{an}前n項和為Sn , 點(n,Sn)(n∈N*)均在y=f(x)的圖象上.
(1)求數列{an}的通項公式;
(2)設 ![]() ,Tn是數列{bn}的前n項和,求當
,Tn是數列{bn}的前n項和,求當 ![]() 對所有n∈N*都成立m取值范圍.
對所有n∈N*都成立m取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
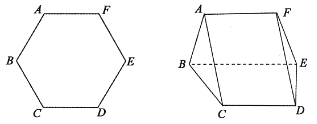
【題目】如圖,將邊長為2的正六邊形ABCDEF沿對角線BE翻折,連接AC、FD,形成如圖所示的多面體,且![]() ,(1)證明:平面ABEF
,(1)證明:平面ABEF![]() 平面BCDE; (2)求DE與平面ABC所成角的正弦值。
平面BCDE; (2)求DE與平面ABC所成角的正弦值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
, ![]() .
.
(1)若曲線![]() 與
與![]() 在公共點
在公共點![]() 處有相同的切線,求實數
處有相同的切線,求實數![]() 的值;
的值;
(2)當![]() 時,若曲線
時,若曲線![]() 與
與![]() 在公共點
在公共點![]() 處有相同的切線,求證:點
處有相同的切線,求證:點![]() 唯一;
唯一;
(3)若![]() ,
, ![]() ,且曲線
,且曲線![]() 與
與![]() 總存在公切線,求:正實數
總存在公切線,求:正實數![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
, ![]() .
.
(1)當![]() 時,求函數
時,求函數![]() 的最小值;
的最小值;
(2)當![]() 時,討論函數
時,討論函數![]() 的單調性;
的單調性;
(3)是否存在實數![]() ,對任意的
,對任意的![]() ,
, ![]() ,且
,且![]() ,有
,有![]() 恒成立,若存在求出
恒成立,若存在求出![]() 的取值范圍,若不存在,說明理由.
的取值范圍,若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com