
【題目】已知函數![]() ,
, ![]() .
.
(1)若曲線![]() 與
與![]() 在公共點
在公共點![]() 處有相同的切線,求實數
處有相同的切線,求實數![]() 的值;
的值;
(2)當![]() 時,若曲線
時,若曲線![]() 與
與![]() 在公共點
在公共點![]() 處有相同的切線,求證:點
處有相同的切線,求證:點![]() 唯一;
唯一;
(3)若![]() ,
, ![]() ,且曲線
,且曲線![]() 與
與![]() 總存在公切線,求:正實數
總存在公切線,求:正實數![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)證明見解析;(3)1.
;(2)證明見解析;(3)1.
【解析】試題分析:(1)![]() 曲線
曲線![]() 與
與![]() 在公共點
在公共點![]() 處有相同的切線,
處有相同的切線, 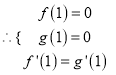 ,解出即可;(2)設
,解出即可;(2)設![]() ,由題設得
,由題設得![]() ,轉化為關于
,轉化為關于![]() 的方程只有一解,進而構造函數轉化為函數只有一個零點,利用導數即可證明;(3)設曲線
的方程只有一解,進而構造函數轉化為函數只有一個零點,利用導數即可證明;(3)設曲線![]() 在點
在點![]() 處的切線方程為
處的切線方程為![]() ,則只需使該切線與
,則只需使該切線與![]() 相切即可,也即方程組
相切即可,也即方程組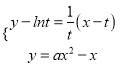 ,只有一解即可,所以消去
,只有一解即可,所以消去![]() 后
后![]() ,問題轉化關于
,問題轉化關于![]() 方程總有解,分情況借助導數進行討論即可求得
方程總有解,分情況借助導數進行討論即可求得![]() 值.
值.
試題解析:(1)![]() ,
,![]() .∵曲線
.∵曲線![]() 與
與![]() 在公共點
在公共點![]() 處有相同的切線∴
處有相同的切線∴ 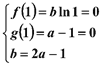 , 解得,
, 解得,![]() .
.
(2)設![]() ,則由題設有
,則由題設有![]() … ①又在點
… ①又在點![]() 有共同的切線
有共同的切線
∴![]() 代入①得
代入①得 ![]()
設![]() ,則
,則![]() ,
,
∴![]() 在
在![]() 上單調遞增,所以
上單調遞增,所以 ![]() =0最多只有
=0最多只有![]() 個實根,
個實根,
從而,結合(Ⅰ)可知,滿足題設的點![]() 只能是
只能是![]()
(3)當![]() ,
,![]() 時,
時,![]() ,
,![]() ,
,
曲線![]() 在點
在點![]() 處的切線方程為
處的切線方程為![]() ,即
,即![]() .
.
由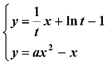 ,得
,得 ![]() .
.
∵ 曲線![]() 與
與![]() 總存在公切線,∴ 關于
總存在公切線,∴ 關于![]()
![]() 的方程
的方程![]() ,
,
即![]()
![]() 總有解.
總有解.
若![]() ,則
,則![]() ,而
,而![]() ,顯然
,顯然![]() 不成立,所以
不成立,所以 ![]() .
.
從而,方程![]() 可化為
可化為 ![]() .
.
令![]()
![]() ,則
,則![]() .
.
∴ 當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ,即
,即 ![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增.∴
上單調遞增.∴![]() 在
在![]() 的最小值為
的最小值為![]() ,
,
所以,要使方程![]() 有解,只須
有解,只須![]() ,即
,即![]() .
.


 期末沖刺100分創新金卷完全試卷系列答案
期末沖刺100分創新金卷完全試卷系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓C1: ![]() (a>b>0)的離心率為
(a>b>0)的離心率為 ![]() ,且過點(1,
,且過點(1, ![]() ).
).
(1)求C1的方程;
(2)設直線l同時與橢圓C1和拋物線C2:y2=4x相切,求直線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數y=f(x)對任意的x∈(﹣ ![]() ,
, ![]() )滿足f′(x)cosx+f(x)sinx>0(其中f′(x)是函數f(x)的導函數),則下列不等式成立的是( )
)滿足f′(x)cosx+f(x)sinx>0(其中f′(x)是函數f(x)的導函數),則下列不等式成立的是( )
A.![]() f(﹣
f(﹣ ![]() )<f(﹣
)<f(﹣ ![]() )
)
B.![]() f(
f( ![]() )<f(
)<f( ![]() )??
)??
C.f(0)>2f( ![]() )
)
D.f(0)> ![]() f(
f( ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C中心在原點,焦點在坐標軸上,且該橢圓經過點( ![]() ,
, ![]() )和點
)和點 ![]() .求
.求
(1)橢圓C的方程;
(2)P,Q,M,N四點在橢圓C上,F1為負半軸上的焦點,直線PQ,MN都過F1且 ![]() ,求四邊形PMQN的面積最小值和最大值.
,求四邊形PMQN的面積最小值和最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線的頂點在原點,焦點在x軸,且拋物線上點P(2,m)到焦點的距離為3,斜率為2的直線L與拋物線相交于A,B兩點且|AB|=3 ![]() ,求拋物線和直線L的方程.
,求拋物線和直線L的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() =1(a>b>0)的左、右焦點為F1、F2 , 離心率為e.直線l:y=ex+a與x軸、y軸分別交于點A、B,M是直線l與橢圓C的一個公共點,P是點F1關于直線l的對稱點,設
=1(a>b>0)的左、右焦點為F1、F2 , 離心率為e.直線l:y=ex+a與x軸、y軸分別交于點A、B,M是直線l與橢圓C的一個公共點,P是點F1關于直線l的對稱點,設 ![]() =λ
=λ ![]() .
.
(1)證明:λ=1﹣e2;
(2)若λ= ![]() ,△MF1F2的周長為6;寫出橢圓C的方程;
,△MF1F2的周長為6;寫出橢圓C的方程;
(3)確定λ的值,使得△PF1F2是等腰三角形.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】綜合題。
(1)現有5名男生和3名女生.若從中選5人,且要求女生只有2名,站成一排,共有多少種不同的排法?
(2)從{﹣3,﹣2,﹣1,0,1,2,3,4}中任選三個不同元素作為二次函數y=ax2+bx+c的系數,問能組成多少條經過原點且頂點在第一象限或第三象限的拋物線?
(3)已知( ![]() +2x)n , 若展開式中第5項、第6項與第7項的二項式系數成等差數列,求展開式中二項式系數最大項的系數.
+2x)n , 若展開式中第5項、第6項與第7項的二項式系數成等差數列,求展開式中二項式系數最大項的系數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com