
分析 (1)利用等差數列的通項公式及其前n項和公式結合已知列式求得首項和公差,則an可求;
(2)由(1)知數列{an}的前5項為5,4,3,2,1,可知:等比數列{bn}的前3項為4,2,1.首項為4,公比為$\frac{1}{2}$,可得bn.利用“錯位相減法”可得Tn .
解答 解:(1)設等差數列{an}的首項為a1,公差為d,
由a6=0,S4=14,得$\left\{\begin{array}{l}{{a}_{1}+5d=0}\\{4{a}_{1}+6d=14}\end{array}\right.$,解得a1=5,d=-1.
∴an=5-(n-1)=6-n;
(2)由(1)知數列{an}的前5項為5,4,3,2,1,
∴等比數列{bn}的前3項為4,2,1,
首項為4,公比為$\frac{1}{2}$.
∴${b}_{n}=4•(\frac{1}{2})^{n-1}$,
∴${a}_{n}{b}_{n}=4(6-n)•(\frac{1}{2})^{n-1}$,
數列{anbn}的前n項和Tn,
則$\frac{1}{4}{T}_{n}=5+4•\frac{1}{2}+3•(\frac{1}{2})^{2}+…+$(6-n)•$(\frac{1}{2})^{n-1}$,
$\frac{1}{8}{T}_{n}$=5$•\frac{1}{2}$+4$•(\frac{1}{2})^{2}$+…+(7-n)•$(\frac{1}{2})^{n-1}$+(6-n)•$(\frac{1}{2})^{n}$,
∴$\frac{1}{8}{T}_{n}$=5-[$\frac{1}{2}+(\frac{1}{2})^{2}+…+(\frac{1}{2})^{n-1}$]-(6-n)•$(\frac{1}{2})^{n}$
=5-$\frac{\frac{1}{2}[1-(\frac{1}{2})^{n-1}]}{1-\frac{1}{2}}-(6-n)•(\frac{1}{2})^{n}$=4+(n-4)$•(\frac{1}{2})^{n}$.
∴${T}_{n}=32+8(n-4)•(\frac{1}{2})^{n}$.
點評 本題考查了等差數列與等比數列的通項公式及其前n項和公式,訓練了錯位相減法求數列的通項公式,考查了推理能力與計算能力,屬于中檔題.


 導學教程高中新課標系列答案
導學教程高中新課標系列答案 小學課時特訓系列答案
小學課時特訓系列答案科目:高中數學 來源: 題型:解答題
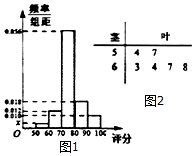 某單位為了解甲、乙兩部門對本單位職工的服務情況,隨機訪問50名職工.已知50名職工對甲、乙兩部門的評分都在區間[50,100]內,根據50名職工對甲部門的評分繪制的頻率分布直方圖,以及根據50名職工對乙部門評分中落在[50,60),[60,70)內的所有數據繪制的莖葉圖,如圖所示.
某單位為了解甲、乙兩部門對本單位職工的服務情況,隨機訪問50名職工.已知50名職工對甲、乙兩部門的評分都在區間[50,100]內,根據50名職工對甲部門的評分繪制的頻率分布直方圖,以及根據50名職工對乙部門評分中落在[50,60),[60,70)內的所有數據繪制的莖葉圖,如圖所示.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
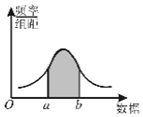
| A. | 組距越大,頻率分布折線圖越接近于它 | |
| B. | 樣本容量越小,頻率分布折線圖越接近于它 | |
| C. | 陰影部分的面積代表總體在(a,b)內取值的百分比 | |
| D. | 陰影部分的平均高度代表總體在(a,b)內取值的百分比 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -$\frac{1}{2}$ | B. | -2 | C. | 2 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
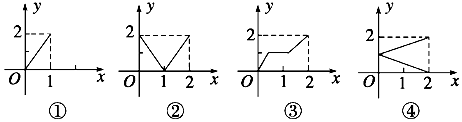
| A. | ①②③④ | B. | ①②③ | C. | ②③ | D. | ② |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com